1) 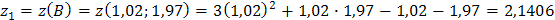
2) Т.к. приращение функции двух переменных
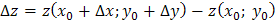 приближенно равно дифференциалу этой функции при
приближенно равно дифференциалу этой функции при 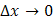 и
и 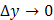 :
: 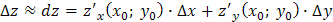 ,
,
то 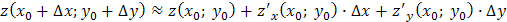 .
.
Т.е. 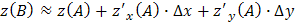 .
.
Имеем 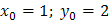 ;
; 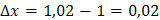 ;
; 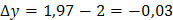 ;
;
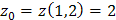 ;
; 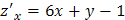 ;
; 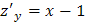 ;
; 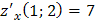 ;
; 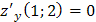 . Итак, приближенные значения функции в точке
. Итак, приближенные значения функции в точке 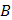
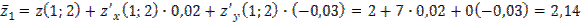 .
.
3) Найдем относительную погрешность 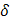 при замене
при замене 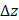 на
на 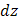 :
:
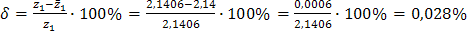
4) Т.к. уравнение касательной плоскости к поверхности 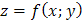 в точке
в точке 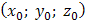 имеет вид
имеет вид 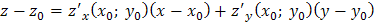 ;
;
то имеем 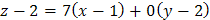 или
или 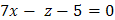
Задача 13. Найти наименьшее и наибольшее значение функции 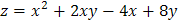 в замкнутой области
в замкнутой области 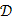 , заданной системой неравенств
, заданной системой неравенств 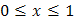 ,
, 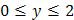 . Сделать чертеж.
. Сделать чертеж.
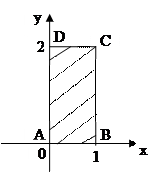 |
Решение. Найдем стационарные точки функции внутри области 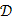 , решая систему
, решая систему 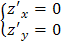 . Имеем,
. Имеем, 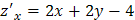 ,
, 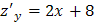 , тогда решение системы
, тогда решение системы 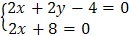 есть точка
есть точка 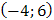 . Но она не входит в область
. Но она не входит в область 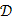 .
.
Исследуем теперь поведение функции на границе области 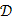 . Найдем сначала стационарные точки функции внутри отрезков границы области.
. Найдем сначала стационарные точки функции внутри отрезков границы области.
а) Уравнение стороны 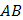 прямоугольника:
прямоугольника: 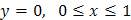 .
.
На стороне 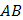 функция
функция 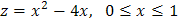 .
.
Найдем стационарные точки внутри отрезка 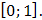
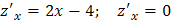 при
при 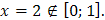
б) Уравнение стороны 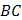 :
: 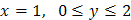 .
.
На стороне 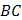 прямоугольника функция
прямоугольника функция 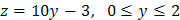 .
.
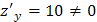 , т.е. стационарных точек нет.
, т.е. стационарных точек нет.
в) Уравнение стороны 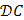 :
: 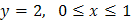 .
.
На стороне 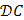 прямоугольника функция
прямоугольника функция 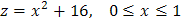 .
.
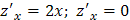 при
при 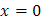 , т.е. внутри отрезка
, т.е. внутри отрезка 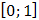 стационарных точек нет.
стационарных точек нет.
г) Уравнение стороны 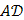 :
: 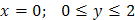 .
.
На стороне 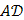 функция
функция 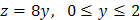 ,
, 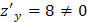 , т.е. стационарных точек нет.
, т.е. стационарных точек нет.
Итак, функция не имеет стационарных точек ни внутри области 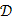 , ни внутри отрезков границы области
, ни внутри отрезков границы области 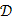 .
.
Найдем значения функции в вершинах прямоугольника 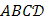 и выберем среди них наименьшее и наибольшее.
и выберем среди них наименьшее и наибольшее.
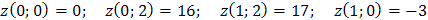 .
.
Итак, 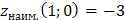 ,
, 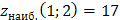
Задача 14. Даны функция 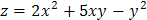 , точка
, точка 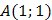 и вектор
и вектор 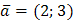 . Найти:
. Найти:
1) 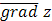 в точке
в точке 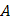 ;
;
2) производную в точке 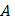 по направлению вектора
по направлению вектора 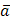 .
.
 2015-03-07
2015-03-07 480
480








