Задача 1. Даны векторы 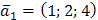 ,
, 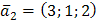 ,
, 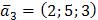 и
и 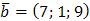 в некотором базисе трехмерного пространства. Показать, что векторы
в некотором базисе трехмерного пространства. Показать, что векторы 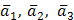 образуют базис данного трехмерного пространства и найти координаты вектора
образуют базис данного трехмерного пространства и найти координаты вектора 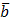 в этом базисе.
в этом базисе.
Решение. Векторы 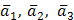 образуют базис, если они линейно независимы. Составим векторное равенство
образуют базис, если они линейно независимы. Составим векторное равенство 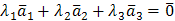 . Записывая
. Записывая 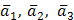 в виде векторов – столбцов, получим
в виде векторов – столбцов, получим 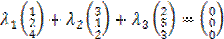 . Задача свелась, таким образом, к решению системы
. Задача свелась, таким образом, к решению системы 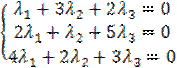 . Решим систему методом Гаусса.
. Решим систему методом Гаусса. 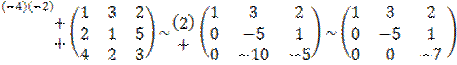 . Итак, система приведена к виду
. Итак, система приведена к виду 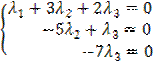 . Полученная система имеет единственное нулевое решение:
. Полученная система имеет единственное нулевое решение: 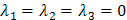 , т.е. векторы
, т.е. векторы 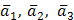 линейно независимы и, следовательно, составляют базис. Вектор
линейно независимы и, следовательно, составляют базис. Вектор 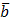 можно представить в виде
можно представить в виде 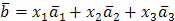 , т.е. координаты вектора
, т.е. координаты вектора 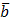 в этом базисе
в этом базисе 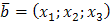 . Для отыскания координат вектора
. Для отыскания координат вектора 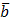 решим систему линейных уравнений методом Гаусса:
решим систему линейных уравнений методом Гаусса: 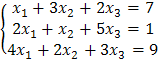 .
.
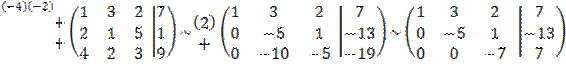 .
.
Итак, система приведена к виду 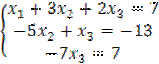 .
.
Находим 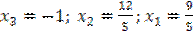 . т.е. вектор
. т.е. вектор 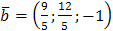 .
.
Задача 2. Даны векторы 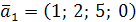 ,
, 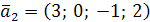 ,
, 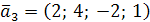 ,
, 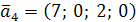 и
и 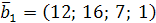 . Показать, что векторы
. Показать, что векторы 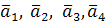 образуют базис четырехмерного пространства, и найти координаты вектора
образуют базис четырехмерного пространства, и найти координаты вектора 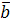 в этом базисе.
в этом базисе.
Решение. Векторы 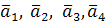 образуют базис, если они линейно независимы. Составим векторное равенство
образуют базис, если они линейно независимы. Составим векторное равенство 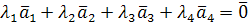 . Записывая
. Записывая 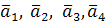 в виде векторов – столбцов, получим
в виде векторов – столбцов, получим 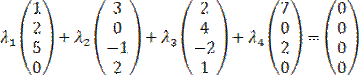 .
.
Задача свелась, таким образом, к решению системы
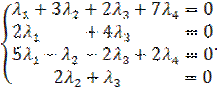
Решим систему методом Гаусса.
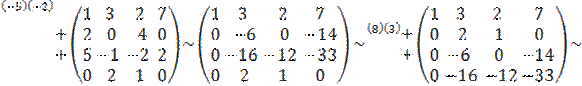
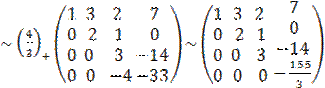 . Итак, система приведена к виду
. Итак, система приведена к виду 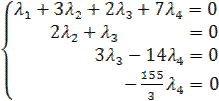 .
.
Полученная система имеет единственное нулевое решение: 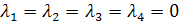 , т.е. векторы
, т.е. векторы 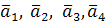 линейно независимы и, следовательно, составляют базис. Вектор
линейно независимы и, следовательно, составляют базис. Вектор 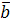 можно представить в виде
можно представить в виде 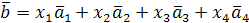 , т.е. координаты вектора
, т.е. координаты вектора 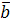 в этом базисе
в этом базисе 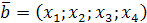 . Для отыскания координат вектора
. Для отыскания координат вектора 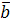 решим систему линейных уравнений методом Гаусса:
решим систему линейных уравнений методом Гаусса: 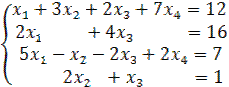 .
.
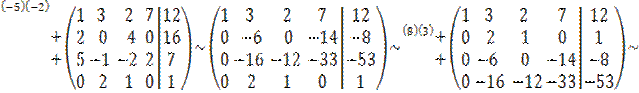
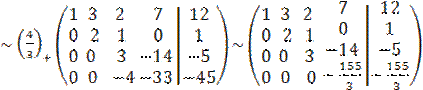 .
.
Итак, система приведена к виду 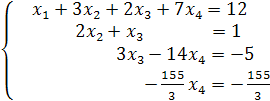 .
.
Находим 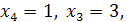
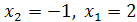 , т.е. вектор
, т.е. вектор 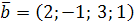 .
.
Задача 3. Даны вершины треугольника 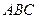 :
: 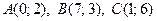 . Найти: 1) длину стороны
. Найти: 1) длину стороны 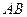 ; 2) внутренний угол
; 2) внутренний угол 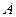 в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину
в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину 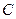 ; 4) уравнение медианы, проведенной через вершину
; 4) уравнение медианы, проведенной через вершину 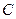 ; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины
; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины 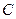 ; 7) систему неравенств, определяющих треугольник
; 7) систему неравенств, определяющих треугольник 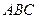
Решение. 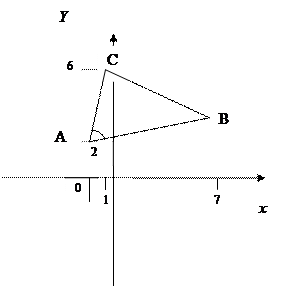

1) Длину стороны 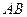 (длина вектора
(длина вектора 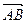 ) находим как расстояние между двумя точками плоскости
) находим как расстояние между двумя точками плоскости 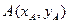 и
и 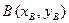 :
: 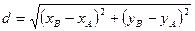 .
.
Поэтому 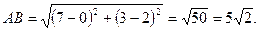
2) Угол 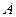 – это угол между векторами
– это угол между векторами 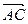 и
и 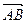 . Координаты этих векторов:
. Координаты этих векторов: 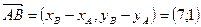 ,
, 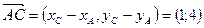 . Таким образом
. Таким образом 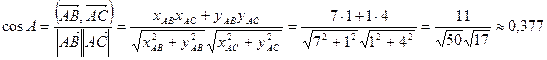 .
.
Таким образом, получаем 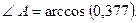
3) Составим уравнение стороны 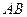 :
: 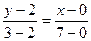 , или
, или 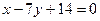 . Угловой коэффициент стороны
. Угловой коэффициент стороны 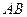 равен
равен 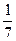 ; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины
; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины 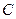 , равен
, равен 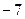 . Уравнение этой высоты имеет вид
. Уравнение этой высоты имеет вид 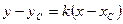 , получаем
, получаем 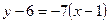 , или
, или 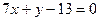 .
.
4) Пусть точка М середина стороны 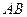 . Найдем ее координаты:
. Найдем ее координаты:
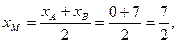
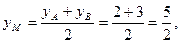 т.
т. 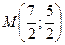 .
.
Уравнение медианы 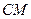 находим с помощью уравнения прямой, проходящей через две данные точки:
находим с помощью уравнения прямой, проходящей через две данные точки: 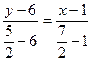 , получим
, получим 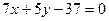 .
.
5) Составим уравнение еще одной высоты треугольника 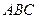 . Например, выберем высоту, проведенную из вершины
. Например, выберем высоту, проведенную из вершины 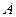 . Аналогично пункту 3) составим уравнение стороны
. Аналогично пункту 3) составим уравнение стороны 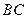 :
:
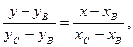
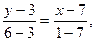
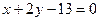 .
.
Угловой коэффициент стороны 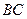 равен
равен 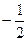 ; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины
; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины 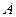 , равен
, равен 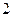 . Уравнение этой высоты имеет вид
. Уравнение этой высоты имеет вид 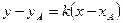 , получаем
, получаем 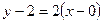 , или
, или 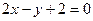 . Поскольку мы ищем точку пересечения высот треугольника, то координаты этой точки должны удовлетворять системе уравнений
. Поскольку мы ищем точку пересечения высот треугольника, то координаты этой точки должны удовлетворять системе уравнений 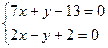 ;
; 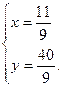 . Таким образом точка пересечения высот треугольника
. Таким образом точка пересечения высот треугольника  имеет координаты
имеет координаты 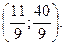
6) Найдем длину высоты, опущенной из вершины 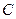 по формуле расстояния от точки
по формуле расстояния от точки 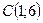 до прямой
до прямой 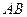 :
: 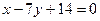 :
: 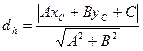 . Таким образом
. Таким образом
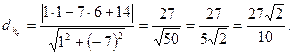
7) Стороны треугольника 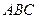 заданы уравнениями прямых:
заданы уравнениями прямых:
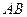 :
: 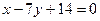 ; (см. пункт 3).
; (см. пункт 3).
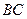 :
: 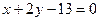 ; (см. пункт 5).
; (см. пункт 5).
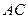 :
: 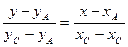 ;
; 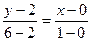 ;
; 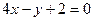 .
.
Каждая из этих прямых делит координатную плоскость на две полуплоскости. Область треугольника 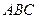 лежит выше прямой
лежит выше прямой 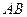 , т.е. в полуплоскости, которая задается неравенством:
, т.е. в полуплоскости, которая задается неравенством: 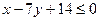 . Прямая
. Прямая 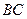 делит координатную плоскость на две полуплоскости, нам необходима та, которая удовлетворяет неравенству:
делит координатную плоскость на две полуплоскости, нам необходима та, которая удовлетворяет неравенству: 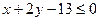 . Из двух полуплоскостей, которые разделяет прямая
. Из двух полуплоскостей, которые разделяет прямая 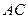 , выбираем ту, которая задается неравенством:
, выбираем ту, которая задается неравенством: 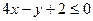 .
.
Таким образом, область треугольника  , определяется системой неравенств:
, определяется системой неравенств: 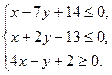
Задача 4. Даны координаты вершин пирамиды  :
: 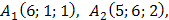
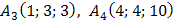 . Найти:
. Найти:
1) длину ребра 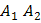 ;
;
2) угол между ребрами 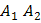 и
и 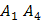 ;
;
3) угол между ребром 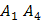 и гранью
и гранью 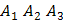 ;
;
4) площадь грани 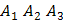 ;
;
5) объем пирамиды; 6) уравнение прямой 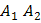 ;
;
7) уравнение плоскости 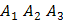 ;
;
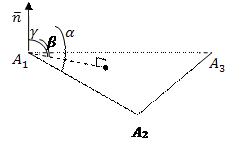
 8) уравнение высоты, опущенной из вершины
8) уравнение высоты, опущенной из вершины 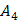 на грань
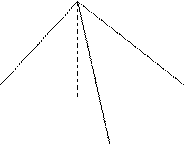
на грань 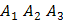 . Сделать чертеж.
. Сделать чертеж.
|
 |
1) Длина ребра 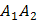 есть длина вектора
есть длина вектора 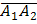 , координаты которого
, координаты которого 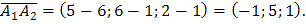 Т.к. длина вектора
Т.к. длина вектора 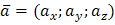 находится по формуле
находится по формуле 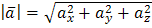 , то
, то 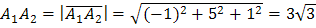 .
.
2) Угол 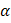 между ребрами
между ребрами 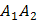 и
и 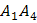 есть угол между векторами
есть угол между векторами
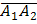 =(-1,5,1) и
=(-1,5,1) и 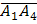 =(4-6;4-1;10-1)=(-2;3;9), поэтому
=(4-6;4-1;10-1)=(-2;3;9), поэтому 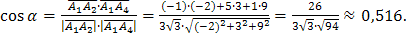
Отсюда 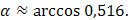
3) Обозначим угол между ребром 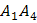 и гранью
и гранью 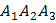 через
через 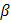 , тогда
, тогда 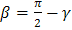 , где
, где 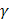 – угол между вектором
– угол между вектором 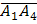 =(-2;3;9) и нормальным вектором
=(-2;3;9) и нормальным вектором 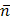 плоскости
плоскости 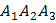 , которым является, например, векторное произведение векторов
, которым является, например, векторное произведение векторов 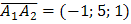 и
и 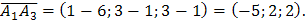
Т.к. векторное произведение векторов 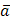 =(
=(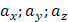 ) и
) и 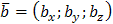 находится по формуле
находится по формуле 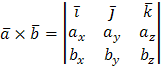 , то
, то 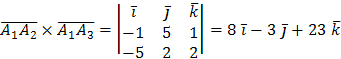 . Итак,
. Итак, 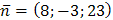 . Найдем теперь угол
. Найдем теперь угол 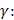
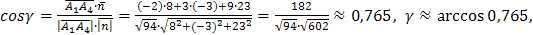 значит
значит
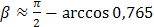 или
или 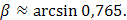
4) Т.к. длина векторного произведения двух векторов равна площади параллелограмма, построенного на этих векторах, как на сторонах, то площадь S грани 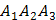 (площадь треугольника) найдем как половину площади параллелограмма, построенного на векторах
(площадь треугольника) найдем как половину площади параллелограмма, построенного на векторах 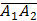 и
и 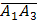 как на сторонах, т.е. как половину длины векторного произведения этих векторов.
как на сторонах, т.е. как половину длины векторного произведения этих векторов.
Т.к. 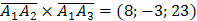 (см. пункт 3), то
(см. пункт 3), то
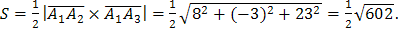
5) Т.к. объем V треугольной пирамиды, построенной на векторах 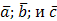 , находится по формуле
, находится по формуле 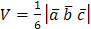 , где
, где 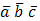 - смешанное произведение векторов
- смешанное произведение векторов 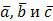 , то
, то
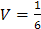
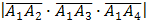 . Найдем смешанное произведение векторов
. Найдем смешанное произведение векторов
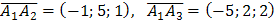 и
и 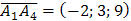 по формуле
по формуле
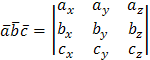 :
:
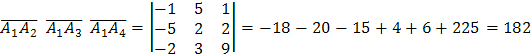 (определитель вычислен по схеме треугольников). Итак,
(определитель вычислен по схеме треугольников). Итак, 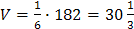 .
.
6) Т.к. уравнение прямой, проходящей через точку 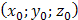 параллельно вектору
параллельно вектору 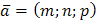 имеет вид
имеет вид 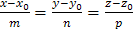 , то уравнение прямой
, то уравнение прямой 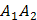 найдем как уравнение прямой, проходящей через точку
найдем как уравнение прямой, проходящей через точку 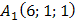 в направлении вектора
в направлении вектора 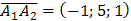 :
: 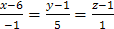 .
.
7) Т.к. уравнение плоскости, проходящей через точку 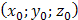 перпендикулярно вектору
перпендикулярно вектору 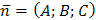 имеет вид
имеет вид 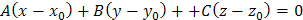 (
(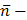 нормальный вектор плоскости), то уравнение плоскости
нормальный вектор плоскости), то уравнение плоскости 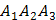 найдем как уравнение плоскости, проходящей через точку
найдем как уравнение плоскости, проходящей через точку 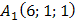 с нормальным вектором
с нормальным вектором 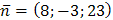 (см. пункт 3):
(см. пункт 3):
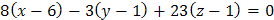 или
или 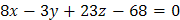
8) Уравнение высоты, опущенной из вершины 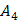 на грань
на грань 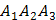 , найдем как уравнение прямой, проходящей через точку
, найдем как уравнение прямой, проходящей через точку 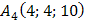 в направлении вектора
в направлении вектора 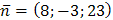 -нормального вектора плоскости
-нормального вектора плоскости 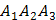 (см. пункт 3):
(см. пункт 3): 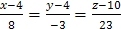 .
.
Задача 5. Найти матрицу, обратную матрице 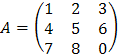 . Проверить результат, вычислив произведение данной и обратной матриц.
. Проверить результат, вычислив произведение данной и обратной матриц.
Решение. Определитель матрицы 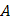
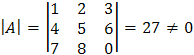 , значит обратная матрица
, значит обратная матрица 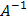 существует. Найдем матрицу
существует. Найдем матрицу 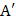 , транспонированную к
, транспонированную к 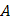 :
: 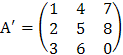 . Найдем алгебраические дополнения всех элементов матрицы
. Найдем алгебраические дополнения всех элементов матрицы 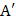 и составим из них присоединенную матрицу
и составим из них присоединенную матрицу 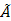 .
.
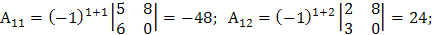
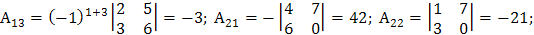
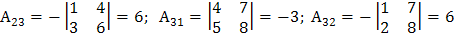
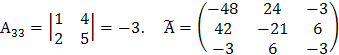 .
.
Найдем обратную матрицу 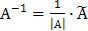 :
:
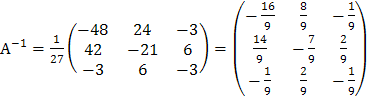 .
.
Проверка:
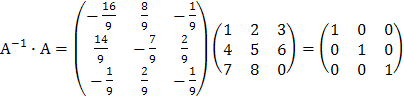 .
.
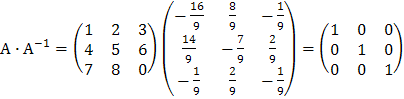 .
.
Задача 6. Дана система линейных уравнений
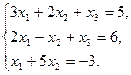
Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
Решение. 1) Докажем совместность системы. Для этого вычислим ранг матрицы А исходной системы и ранг расширенной матрицы системы 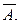
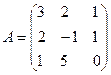
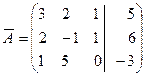

Для удобства вычислений элементарные преобразования будем производить с матрицей 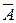 :
:










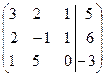 ~
~ 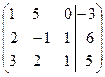 ~
~ 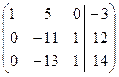 ~
~ 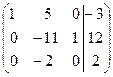
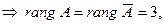 т.е. по теореме Кронекера–Капелли система совместна.
т.е. по теореме Кронекера–Капелли система совместна.
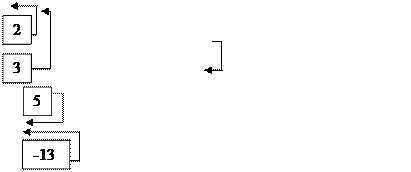
2) Решим систему методом Гаусса. Для этого матрицу 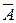 приведем к диагональному виду:
приведем к диагональному виду:
|
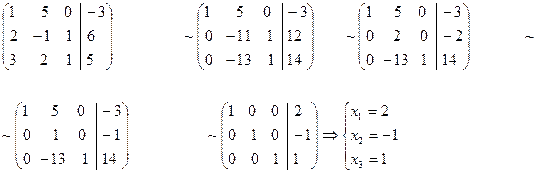
3) Решим систему матричным способом. Для этого введем следующие матрицы и исходную систему запишем в матричном виде.
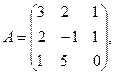
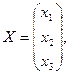
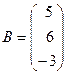 .
.
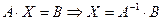
Вычислим обратную матрицу 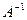 . Определитель матрицы А
. Определитель матрицы А 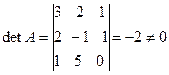 , значит обратная матрица существует. Затем, вычислив к каждому элементу матрицы А алгебраические дополнения, составим из них матрицу
, значит обратная матрица существует. Затем, вычислив к каждому элементу матрицы А алгебраические дополнения, составим из них матрицу 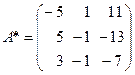 , транспонируем ее
, транспонируем ее 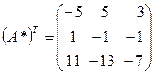 и находим обратную матрицу
и находим обратную матрицу 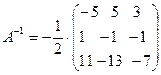
 .
.
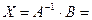
= 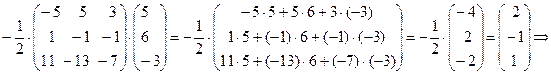
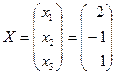 .
.
Ответ: 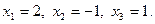
Задача 7. Найти пределы функций, не пользуясь правилом Лопиталя.
а) 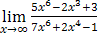 ; б)
; б) 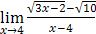 ; в)
; в) 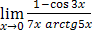 ; г)
; г) 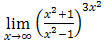 .
.
Решение. а) Для раскрытия неопределенности  разделим числитель и знаменатель дроби на высшую степень (на
разделим числитель и знаменатель дроби на высшую степень (на 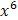 ):
):
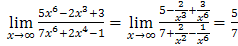 . Здесь учитывалось стремление к нулю дробей
. Здесь учитывалось стремление к нулю дробей 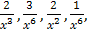 как обратных к бесконечно большим функциям.
как обратных к бесконечно большим функциям.
б) Для раскрытия неопределенности 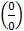 умножим и разделим на выражение, сопряженное числителю, т.е. на
умножим и разделим на выражение, сопряженное числителю, т.е. на 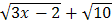 :
:
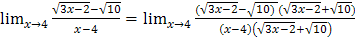 =
=
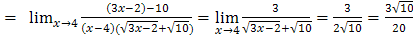 .
.
Использовалась формула 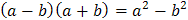 .
.
в) Для раскрытия неопределенности 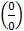 воспользуемся эквивалентностями (следствиями первого замечательного предела):
воспользуемся эквивалентностями (следствиями первого замечательного предела): 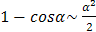 и
и 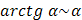 при
при 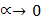 и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:
и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:
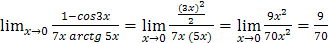 .
.
г) Для раскрытия неопределенности 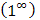 преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:
преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:
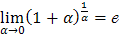 .
.
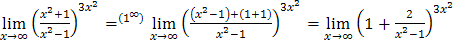 =
=
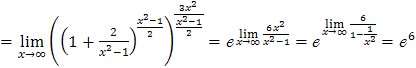 .
.
Здесь бесконечно малой величиной 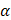 является выражение
является выражение 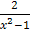 .
.
Задача 8. Найти пределы функций, не пользуясь правилом Лопиталя.
1) 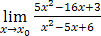 при а)
при а) 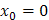 ; б)
; б) 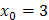 ; в)
; в) 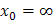 ;
;
2) 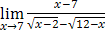 ; 3)
; 3) 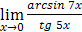 ; 4)
; 4) 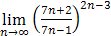 .
.
Решение. 1) а) 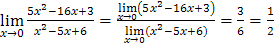 .
.
б) Для раскрытия неопределенности 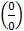 разложим числитель и знаменатель на множители:
разложим числитель и знаменатель на множители:
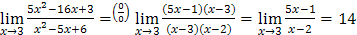 .
.
в) Для раскрытия неопределенности  разделим числитель и знаменатель дроби на высшую степень (на
разделим числитель и знаменатель дроби на высшую степень (на 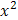 ):
):
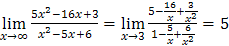 . Здесь учитывалось стремление к нулю дробей
. Здесь учитывалось стремление к нулю дробей 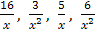 , как обратных к бесконечно большим функциям.
, как обратных к бесконечно большим функциям.
2) Для раскрытия неопределенности 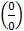 умножим и разделим на выражение, сопряженное знаменателю до разности квадратов
умножим и разделим на выражение, сопряженное знаменателю до разности квадратов
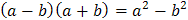 , т.е. на
, т.е. на 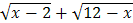 :
:
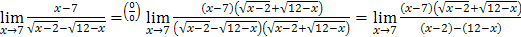 =
=
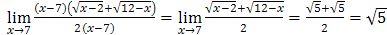
3) Для раскрытия неопределенности 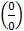 воспользуемся эквивалентностями (следствиями первого замечательного предела):
воспользуемся эквивалентностями (следствиями первого замечательного предела): 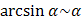 и
и 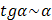 при
при 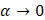 и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:
и тем, что при вычислении предела частного можно одну бесконечно малую величину заменить на ей эквивалентную в этом процессе:
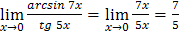 .
.
4) Для раскрытия неопределенности 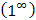 преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:
преобразуем выражение, чтобы воспользоваться следствием второго замечательного предела:
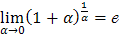 .
.
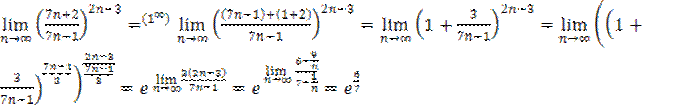 Здесь бесконечно малой величиной
Здесь бесконечно малой величиной 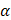 является выражение
является выражение 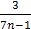 .
.
Задача 9. Найти точки разрыва функции 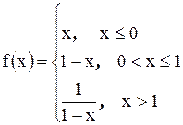
Решение. Так как у данной функции нет точек, в которых она неопределенна, то точками разрыва могут быть либо нули знаменателя, либо точки в которых происходит смена аналитических выражений. В данном случае только точки 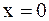 и
и 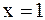 (в остальных точках данная функция непрерывна).
(в остальных точках данная функция непрерывна).
Выясним будет ли 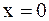 точкой разрыва данной функции. Для этого найдем левосторонний и правосторонний пределы функции в данной точке:
точкой разрыва данной функции. Для этого найдем левосторонний и правосторонний пределы функции в данной точке:
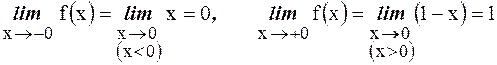 .
.
Так как 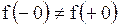 , то
, то 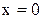 – точка разрыва, причем первого рода, поскольку оба односторонних предела конечные. Этот разрыв не устраним, т.к.
– точка разрыва, причем первого рода, поскольку оба односторонних предела конечные. Этот разрыв не устраним, т.к.
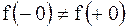 .
.
Точка 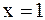 есть точка разрыва данной функции второго рода, т.к.
есть точка разрыва данной функции второго рода, т.к.
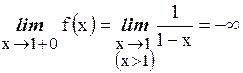 .
.
В данном случае 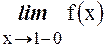 можно не вычислять.
можно не вычислять.
Ответ: 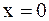 – точка разрыва первого рода,
– точка разрыва первого рода,
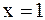 – точка разрыва второго рода.
– точка разрыва второго рода.
 2015-03-07
2015-03-07 9469
9469

 тиии
тиии