1) Вектор 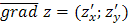 .
.
Находим 

Итак, 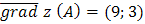
2) Производная функции 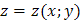 в точке
в точке 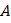 по направлению вектора
по направлению вектора 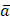 находится по формуле
находится по формуле
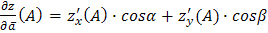 , где
, где
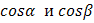 – направляющие косинусы вектора
– направляющие косинусы вектора 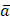 .
.
Находим 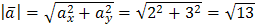 ,
,
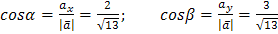 .
.
Тогда 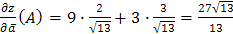 .
.
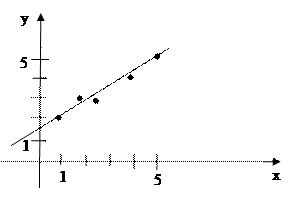
Задача 15. Экспериментально получены пять значений функции 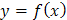 при пяти значениях аргумента, которые записаны в таблице:
при пяти значениях аргумента, которые записаны в таблице:
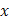
| 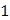
| 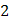
| 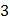
| 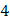
| 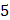
|
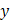
| 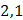
| 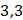
| 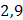
| 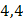
| 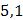
|
Методом наименьших квадратов найти функцию вида 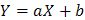 , выражающую (аппроксимирующую) функцию
, выражающую (аппроксимирующую) функцию 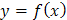 . Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции
. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки и график аппроксимирующей функции 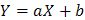 .
.
Решение. Найдем необходимые для расчетов суммы 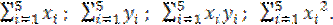
 |
Промежуточные вычисления оформим в виде вспомогательной таблицы.
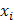
| 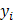
| 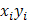
| 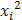
| |
| 2,1 3,3 2,9 4,4 5,1 | 2,1 6,6 8,7 17,6 25,5 | |||
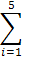
| 17,8 | 60,5 |
Система нормальных уравнений
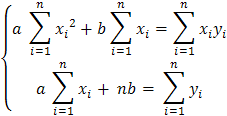
имеет вид 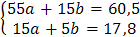 .
.
Ее решение 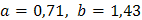 дает искомую зависимость:
дает искомую зависимость: 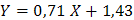 .
.
Задача 16. Найти полный дифференциал функции 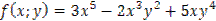 .
.
Решение. Найдем частные производные функции и воспользуемся формулой
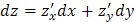 .
.
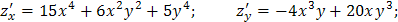
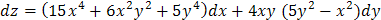 .
.
 2015-03-07
2015-03-07 611
611








