2015-03-27
1018
Расчёт коэффициента теплопроводности снега производится исходя из зависимости плотности снега от температуры воздуха на поверхности снегового покрова. Тогда коэффициент теплопроводности снега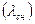 
можно рассчитать по следующим формулам:
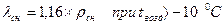
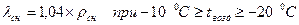
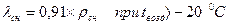
где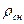 
– плотность снега; 
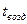– температура воздуха, 
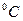. Для упрощения задачи плотность может быть выбрана постоянной и задача сводится к нахождению величины 
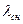для каждой точки снегового покрова в течение определённого промежутка времени с последующим нахождением среднего значения 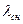за декаду. При этом известно, что оптимальные условия применения задачи следующие:
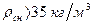
За декаду амплитуда колебаний температуры воздуха должна быть более 10 .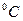
Задача решается (рис. 7) аналогично предыдущей (50) методом сеток, изложенным выше.
Решением является неизвестная величина температуры снега в его слое.
Граничные условия – температура подстилающей поверхности, температура воздуха на поверхности снегового покрова.
Начальные условия – распределение температуры по глубине в первый день наблюдений.
Со стр 25
Рис. 7
Их соотношения определяются из (54).
Таким образом, решение задачи сводится к следующему:
1. Расчёт методом сеток недостающих частей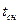 
.
2. Нахождение для каждой 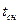коэффициента теплопроводности снега.
3. Расчёт среднего 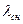для каждого дня и для декады в целом.
Ограничения:
Точность метода: известно, что свежевыпавший снег с плотностью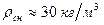 
имеет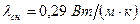 
.
При решении задачи использовались следующие значения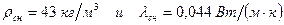 
.
Очевидно, что метод себя оправдывает, сохраняя общие тенденции изменения теплопроводности в зависимости от температуры.
