2015-03-27
595
Метод, основанный на численном решении уравнения турбулентной диффузии, позволяет получать поле концентрации загрязняющего вещества в пределах всей расчётной области, начиная от источника загрязнения до створа водопользования.
Для условий плоской задачи при пренебрежимо малых поперечных скоростях и стационарного во времени процесса уравнение турбулентной диффузии в конечных разностях примет вид (5):
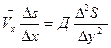. (55)
При расчёте поток в плане разбивается сеткой, каждая вертикальная линия которой отвечает определённому поперечному сечению и предполагается отстоящей от предыдущей и последующей на длине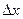 
.
Расстояние между горизонтальными линиями (по ширине реки) равно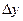 
. Каждой клетке присвоен свой индекс по соответствующим осям координат: по оси 
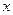- индекс 
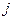, по оси 
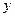- индекс 
.
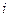На рис. 8 изображена сетка к расчёту турбулентной диффузии (плоская задача).
(здесь должна быть таблица)со стр 28
Рис. 8
Расчётная зависимость, позволяющая вычислить распределение концентраций загрязняющих веществ по длине и ширине потока (плановая или иначе плоская задача), записывается аналогично (41)-(46), т.е.
|
|
|
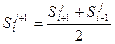
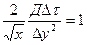(56)
При расчёте по уравнению (56) вся изучаемая область потока или водоёма делится на прямоугольные параллелепипеды, объёмы которых равны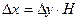 
, 
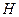– средняя глубина в рассматриваемой области. При пользовании этими формулами предполагается, что уже вблизи от выпуска сточные воды равномерно распространяются по всей глубине .
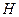Расстояние между расчётными сечениями определяются по формуле
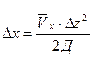(57)
Когда раствор загрязняющего вещества достигает граничных поверхностей потока, для расчёта диффузии следует использовать соотношение, учитывающее отсутствие переноса через стенки потока:
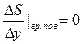(58)
Учёт граничных условий осуществляется путём введения в расчёты экстраполяционных значений концентрации. Расчётная сетка и поле концентрации условно распространяется за ограничивающие поток поверхности. При этом экстраполяционные значения концентрации в клетке, примыкающей к внешней поверхности стенки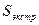 
(рис. 8), и значения концентрации 
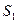в клетке, примыкающей к внутренней поверхности стенки на том же поперечнике, должны удовлетворять условию (57), при решении плоской задачи, что возможно только в случае, если:
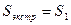(59)
где 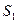- концентрация загрязняющего вещества в потоке к клетке, примыкающей к граничной поверхности. Экстраполяционные значения концентрации используются в расчёте по формуле (56) так же, как и реальные значения. Наглядно это показано на рис. 7.
Начальные условия учитываются при задании места выпуска сточных вод, их расхода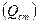 
и их концентрации 
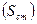. На плане реки (или водоёма) обозначают место сброса и через него проводят начальный поперечник. Ниже по течению поток схематизируется и делится на расчётные клетки. Скорость сточных вод 
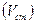, сбрасываемых в водный объект, в месте их поступления принимается равной скорости течения реки 
.
|
|
|
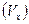Вычисляется условная площадь поперечного сечения притока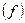 
в месте его падения по следующей зависимости:
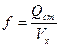(60)
Затем определяется ширина загрязнённой струи в начальном створе:
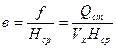(61)
В соответствии с величиной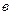 
называется ширина расчётной клетки 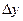. Обычно принимается 
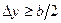, однако если значения оказываются очень большими, то их уменьшают так, чтобы выполнялось неравенство 
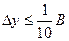(В - средняя ширина реки).
Клетки, попадающие в струю притока сточных вод в начальном поперечнике, заполняются цифрами, выражающими начальную концентрацию сточных вод 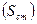, остальные клетки – цифрами, выражающими естественную концентрацию загрязняющего вещества в реке 
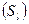(в частном случае это может быть нулевая концентрация).
Часто оказывается удобным вести вычисления в относительных величинах концентрации, например, в % от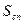 
, полагая 
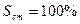. Такой пример позволяет использовать данные расчёта для оценки распределения в потоке любого числа загрязняющих ингредиентов, если будут заданы исходные содержания последних в сточных водах.
