Литература.[1], гл.XI, § 1-5, 6 (пример можно пропустить), упр. 8, 10, 11, 13, 16-21, 23, 24.
Пример. Вычислить 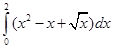 .
.
Решение. Так как интеграл от суммы функций равен сумме интегралов, то
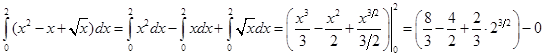
2. Геометрические приложения определенного интеграла
Литература. [1], гл.XII, §1, упр. 1, 3, 5-11; §2, упр. 13, 14, 17, 18; §3, упр. 38-41, 43, 47; §4, 5, упр. 20-23, 25, 32; §6, упр. 49, 51, 53, 56.
Пример 1. Вычислить площадь фигуры, ограниченной линиями 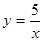 и
и 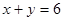 .
.
Решение. Построим в системе координат  эти линии. Найдем точки пересечения этих линий
эти линии. Найдем точки пересечения этих линий

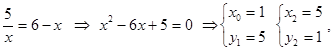
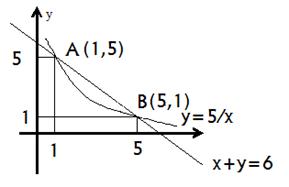
Рис.1.
Обозначим эти точки через A и В. Итак, А(1; 5), В(5; 1). Искомая площадь S равна разности площадей фигур, ограниченных линиями 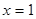 ,
, 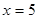 ,
, 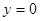 ,
, 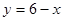 (обозначим эту площадь через S1) и линиями
(обозначим эту площадь через S1) и линиями 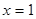 ,
, 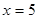 ,
, 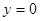 ,
, 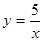 (эту площадь обозначим через S2). Таким образом
(эту площадь обозначим через S2). Таким образом
S = S1 – S2 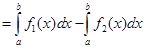
Площадь S2 может быть вычислена с применением определенного интеграла
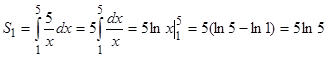 ед 2.
ед 2.
Площадь S1 можно, конечно, вычислить как сумму площадей прямоугольного треугольника и прямоугольника, но удобнее все-таки вычислить S1 как интеграл
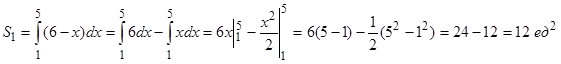 .
.
Теперь можно вычислить и искомую площадь
S = S1 – S2 = 12 – 5 ln5
Ответ: S =12 – 5 ln5 ед 2.
Пример 2. Вычислить объем тела, полученного вращением вокруг оси О 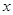 фигуры, ограниченной прямой
фигуры, ограниченной прямой 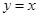 и параболой
и параболой 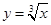 .
.
Решение. Найдем точки пересечения линий. Для этого решим уравнение 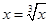 . Получим
. Получим 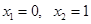 .
.
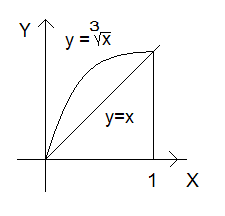
Рис. 2.
Объем тела может быть вычислен по формуле 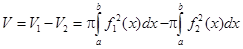 , где
, где
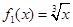 ,
, 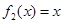 .
.
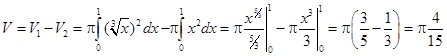 .
.
Ответ: 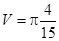 .
.
 2015-03-07
2015-03-07 393
393








