Уравнение с разделенными и разделяющимися переменными

[2, гл. XIII, § 4, упр. 9-16].

Пример 1. Найти общее решение уравнения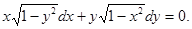

Решение. Сначала определим вид дифференциального уравнения. Данное уравнение не является уравнением с разделенными переменными, так как коэффициенты пр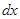и и 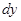зависят каждый от двух переменных. Но, разделив обе части уравнения на произведение 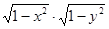(считая, что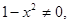 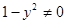), приведем его к виду

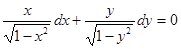
это уравнение с разделенными переменными.

Находим общее решение

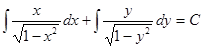
или

.

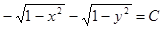Умножив обе части на (-1), включим знак “-“ в постоянную С. Решение примет вид

.

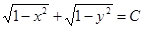Таким образом, нами получено общее решение заданного уравнения.