[2, гл. XVI, § 13, упр. 30, 31, 35-37].
Пример. Определить интервал сходимости ряда
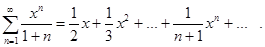
Решение. Коэффициенты ряда 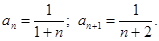 Ищем радиус сходимости
Ищем радиус сходимости 
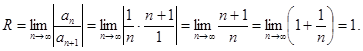
Следовательно, ряд сходится при 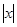 <1 и расходится при
<1 и расходится при 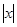 >1. Исследуем отдельно точки
>1. Исследуем отдельно точки 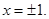
1) 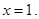 В этой точке ряд равен
В этой точке ряд равен
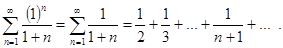
Используем интегральный признак сходимости. Заменим 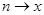 . Тогда
. Тогда
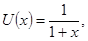
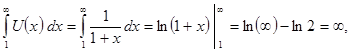
ряд расходится.
2) 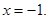 В этой точке ряд равен
В этой точке ряд равен
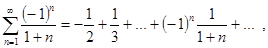
т.е. ряд знакочередующийся. По теореме Лейбница он сходится, действительно, здесь
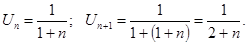
1) 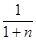 >
> 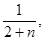 т.е.
т.е. 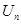 >
> 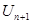 .
.
2) 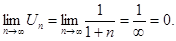
Ряд сходится. Интервал сходимости 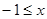 < 1 или
< 1 или 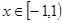 .
.
 2015-03-07
2015-03-07 370
370








