Решение. Приводим задачу к каноническому виду: если знак «≤», то добавляем xi, если знак «≥», то вычитаем xi

Приводим задачу к каноническому виду: если знак «≤», то добавляем x_i, если знак «≥», то вычитаем x_i. Если ищется максимум целевой функции, то коэффициенты при x_i умножаем на (-1) и устремляем функцию к минимуму:

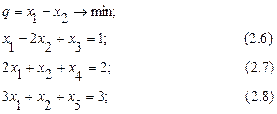
У нас получилось 5 переменных: х₁, х₂, х₃, х₄, х₅. Разбиваем переменные на два вида: базисные и небазисные. Количество базисных переменных равно числу ограничении, т.е. равно трем. Остальные переменные - небазисные.

2. Составляем начальную симплекс таблицу, т. е. выражаем базисные переменные через небазисные, так чтобы свободные члены в уравнении были неотрицательные.

Выразим переменную х₁ из (2.6) и подставим в (2.7) и (2.8). Тогда из (2.7) легко найти х₄, из (2.8) найдем х₅. Подставив x₁ в целевую функцию, получим:

х₁ = 1+2х₂-х₃; (2.9)

x₄= 4 + 3x₂-2x₃; (2.10)

х₅ = 3х₃-7х₂. (2.11)

q= 1+2x₂ – х₃ - х₂ = 1 + х₂ - х₃ → тin;

Получили, что x₁, x₄ и x₅ - базисные переменные, а х₂ и х₃ - небазисные. Затем небазисные переменные х₂ и х₃ приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для первой базисной точки:

x1	x2	x3	х4	х5	q

Полученная базисная точка соответствует координатам точки С(1;0) (см. рис. 1.1). Так как в полученной целевой функции есть отрицательный коэффициент при х₃, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

3. В соответствии с правилом 1 в базис переводим переменную х₃, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a₁₃=1 b₁=1 b₁/a₁₃=1-min,

a₄₃=2 b₄=4 b₄/a₄₃ =2,

а₅₃=-3 b₅=0 a₅₃<0.

Из базиса исключаем x₁, т. к. ему соответствует минимальное значение.

Выражаем переменную х₃ из уравнения (2.9) и подставляем в остальные уравнения и целевую функцию.

q = х₁-х₂→тin;

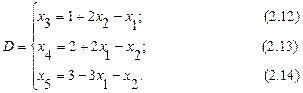
Небазисные переменные x₁ и х₂ приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для базисной точки:

х1	x2	x3	х4	х5	q

Полученная базисная точка соответствует координатам точки C(0; 0) (см. рис. 1.1). Так как в полученной целевой функции есть отрицательные коэффициент при х₂, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

4. В соответствии с правилом 1 в базис переводим переменную х₂, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a₃₂ = -2 b₃ = 1 a₃₂ < 0;

a₄₂ = 1 b₄ = 2 b₃/a₄₂ = 2 – min;

a₅₂ = 1 b₅ = 3 b₅/a₅₂ = 3.

Из базиса исключаем х₄, т. к. ему соответствует минимальное значение.

Выражаем переменную х₂ из уравнения (2.13) и подставляем в остальные уравнения и целевую функцию.

q = - 2 + х₄ – х₁ →min;

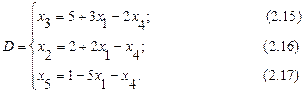
Небазисные переменные x₁ и х₄ приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс таблицу для третьей базисной точки:

x1	x2	x3	х4	х5	q
					-2

Полученная базисная точка соответствует координатам точки A(О; 2) (см. рис. 1.1). Так как в полученной целевой функции есть отрицательный коэффициент при x₁, то оптимальное решение еще не найдено, поэтому переходим к новому базису.

5. В соответствии с правилом 1 в базис переводим переменную x₁, так как она имеет отрицательный знак в целевой функции. В соответствии с правилом 2:

a₃₁ =2 b₃=5 b₃/a₃₁ =5/2,

a₂₁ =1 b₂=2 b₂/a₂₁ =2,

a₅₁ =5 b₅=1 b₅/a₅₁ =1/5 – min,

из базиса исключаем x₅, т. к. ему соответствует минимальное значение.

Выражаем переменную x₁ из уравнения (2.17) и подставляем в остальные уравнения и целевую функцию.

q = -2,2+0,8 х₄+ 0,2 х₅ → min;

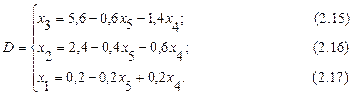
Небазисные переменные х₄ и х₅ приравниваем к нулю, подставляем в получившиеся уравнения и находим значения базисных переменных и целевой функции. Таким образом, получили симплекс-таблицу для четвёртой базисной точки:

х1	х2	хЗ	х4	х5	q
0,2	2,4	5,6			-2, 2

Полученная базисная точка соответствует координатам точки B(0,2; 2,4) (см. рис. 1.1).

Так как полученная целевая функция не содержит отрицательных коэффициентов при х, то оптимальное решение найдено.

Ответ: х₁=0,2; х₂=2,4: q=-22.

Контрольные вопросы и задания

1. Как записывается каноническая форма задачи линейного программирования?

2. Какие переменные называются базисными?

3. В каком случае решение считается найденным?

4. Всегда ли существует решение задачи линейного программирования? В каком случае у задачи нет решения?

5. Какие значения принимают небазисные переменные в базисной точке?