Решение. 1. Определяем входные параметры

1. Определяем входные параметры:

x₁ - количество автомобилей Вольво-850, выпускаемых в неделю

х₂ - количество автомобилей Вольво-940, выпускаемых в неделю

2. Выражение для целевой функции - q=1000x₁+500x₂.

3. Ограничения:

50x₁+20х₂≤1000·40=40000 рабочих часов в неделю (ограничение по квалифицированному труду);

30x₁+40х₂≤900·40=36000 рабочих часов в неделю (ограничение по неквалифицированному труду);

1500x₁+500x₂≤900000 – ограничение по сырью;

$ в неделю

x₁+x₂≤ 210· 5 = 1050- ограничение на доставку авто.

Авто в день дней в неделю авто в неделю

4. Решение задачи в МathCAD.

Записываем начальные значения искомых переменных и выражение для целевой функции с помощью панели «Арифметика» (рис. 1).

Рис.3.1- Панель «Арифметика»

х₁:=1; х₂:=1; q ( х₁, х₂ ): = 100-х₂ + 500-х₂.

В блоке Given записываем ограничения:

x₁≥0; x₂≥0;

50x₁+20х₂≤40000;

30x₁+40х₂≤900·40=36000;

1500x₁+500x₂≤90000;

x₁+x₂≤1050.

Затем переменным х₁ и х₂ присваиваем минимум (максимум) целевой функции q(х₁,х₂) при помощи функции Мinimaze (Махimaze) которая находится на панели инструментов (рис. 2):

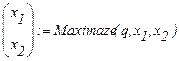
Для получения решения записываем = и нажимаем Enter. После этого полученное x₂ значение подставляем в выражения для q: q(x₁, х₂) = и нажимаем Enter.

Полностью решенная задача в МаthCAD выглядит следующим образом (рис. 3.2).

х₁:=1; х₂:=1;

q ( х₁, х₂ ): = 100-х₂ + 500-х₂.

Given

x₁>0 x₂>0;

50x₁+20х₂≤40000;

30x₁+40х₂≤900·40=36000;

1500x₁+500x₂≤90000.

x₁+x₂≤1050.

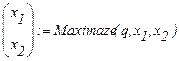
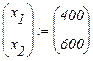
Рис.3.2- Решение задачи

Контрольные вопросы и задания

1. Назовите основные этапы составления модели.

2. В чем состоит отличие целых функций прибыли и затрат?

3. Запишите ограничения на ресурсы в общем виде.

4. В чем смысл ограничений на физическую реализацию?