2015-03-27
284
Основной причиной наличия случайного члена в модели являются несовершенные знания о причинах и взаимосвязях, определяющих то или иное значение зависимой переменной. Поэтому свойства случайных отклонений, в том числе и автокорреляция, в первую очередь зависят от выбора формулы зависимости и состава объясняющих переменных. Так как автокорреляция чаще всего вызывается неправильной спецификацией модели, то необходимо прежде всего скорректировать саму модель. Возможно автокорреляция вызвана отсутствием в модели некоторой важной объясняющей переменной. Следует попытаться определить данный фактор и учесть его в уравнении регрессии. Также можно попробовать изменить формулу зависимости (например, линейную на гиперболическую и т.д.).
Если предложенные методы не устраняют автокорреляцию, значит она обусловлена какими-то внутренними свойствами ряда. В этом случае можно воспользоваться авторегрессионным преобразованием. В линейной регресссионной модели либо в моделях сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка.
|
|
|
Рассмотрим модель парной линейной регрессии
.
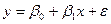Тогда наблюдениям t и (t-1) соответствуют формулы:
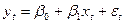(1)
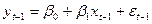. (2)
Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка:
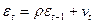, (3)
Где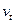 
, t= 2,3, …, T – случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 
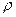известен.
Вычтем из (1) соотношение (2), умноженное на :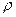
.
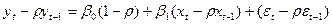Положив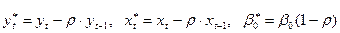 
, и с учетом (3) получим:
.
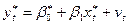Так как по предположению коэффициент 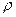известен, то 
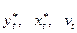вычисляются достаточно просто. В силу того, что случайные отклонения 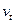удовлетворяют предпосылкам МНК, оценки 
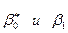будут обладать свойствами наилучших линейных несмещенных оценок.
Однако способ вычисления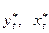 
приводит к потере первого наблюдения. Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Эта проблема обычно преодолевается с помощью поправки Прайса-Винстена:
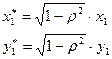
Авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т.е. использовано для уравнения множественной регрессии.
