2015-03-27
574
Однако на практике значение коэффициента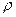 
обычно неизвестно и его необходимо оценивать. Существует несколько методов оценивания:
1. Определение 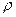на основе статистики Дарбина-Уотсона.
Статистика Дарбина-Уотсона тесно связана с коэффициентом корреляции между соседними отклонениями через соотношение:
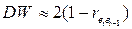. (4)
Тогда в качестве оценки коэффициента 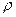может быть взят коэффициент 
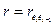. Из (4) имеем:
.
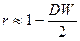Этот метод оценивания эффективен при большом числе наблюдений. В этом случае оценка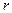 
параметра 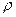будет достаточно точной.
2. Метод Кохрана-Оркатта.
Другим возможным методом оценивания 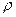является итеративный процесс, называемый методом Кохрана-Оркатта. Опишем данный метод на примере парной регрессии и авторегрессионной схемы первого порядка
.
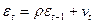1) Оценивается по МНК регрессия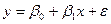 
(*) и для нее определяются оценки 
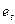отклонений 
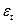, t=1,2, …, T.
2) С использованием авторегрессионной схемы первого порядка оценивается регрессионная зависимость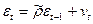 
, где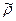 
- оценка коэффициента .
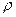3) На основе данной оценки строится уравнение:
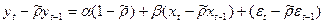, с помощью которого оцениваются коэффициенты α и β (в этом случае 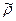известно).
4) Значения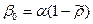 
и β1= β подставляются в уравнение регрессии (*). Вновь вычисляются оценки 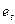отклонений и процесс возвращается к этапу 2.
Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность, т.е. пока разность между предыдущей и последующей оценками 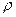не станет меньше любого наперед занятого числа.
3. Метод Хилдрета-Лу.
По данному методу регрессия
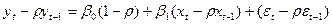оценивается для каждого возможного значения 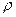из отрезка (-1,1) с любым шагом (например, 0,001; 0,01 и т.д.). Величина 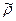, дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента 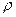. И значения 
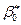и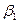 
оцениваются из уравнения регрессии именно с данным значением .
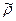Этот итерационный метод широко используется в пакетах прикладных программ.
Таким образом, при установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Если после ряда возможных усовершенствований регрессии (уточнения состава объясняющих переменных, либо измененияформы зависимости) автокорреляция по-прежнему имеет место, то, возможно, это связано с внутренними свойствами ряда отклонений. В этом случае возможны определенные преобразования, устраняющие автокорреляцию. Среди них выделяется авторегрессионная схема первого порядка, которая, может быть обобщена и для множественной регрессии. Дляприменения указанных схем необходимо оценить коэффициент корреляции между отклонениями. Это может быть сделано различными методами: на основе статистики Дарбииа-Уотеона,Кохрана-Оркатта, Хилдрета—Лу и др.
