Теоретическая часть. Системы линейных уравнений вида можно представить в виде матричного уравнения a∙x=b, где a – матрица системы

Системы линейных уравнений вида 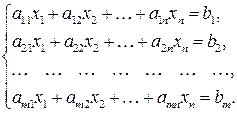можно представить в виде матричного уравнения A∙X=B, где A – матрица системы, состоящая из коэффициентов при неизвестных системы, X – вектор- столбец, составленный из неизвестных x_j, b – вектор-столбец из свободных членов b_i. Такие системырешаются одним из следующих способов:

1) методом Крамера;

2) матричным методом;

3) методом Гаусса, или методом исключения неизвестных.

Решение системы методом Крамера осуществляется по следующему алгоритму:

1. Вводится матрица системы А и вектор-столбец b.

2. Вычисляется определитель матрицы А и сравнивается с нулем (∆≠0).

3. Вычисляются определители матриц ∆i, полученные из матрицы А заменой i -ого столбца столбцом свободных членов.

4. Находится решение системы по формулам Крамера.

Решение системы матричным способом существует, если ∆≠0 и находится с помощью обратной матрицы по формуле 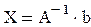. Также решение системы может быть получено с помощью линейной функции lsolve (A,b).

Решение системы линейных уравнений методом Гаусса осуществляется с использованием уже известных нам функций создания расширенной матрицы – augment (A,b)и блока матрицы – submatrix (A, ir, jr, ic, jc), а также функции rref (A), приводящей матрицу к ступенчатому виду с единичной матрицей в первых столбцах. Проверка правильности решения осуществляется умножением матрицы системы на вектор-столбец решения.