Пусть проводится n испытаний, и результатом каждого из них является пара чисел – значения некоторых переменных x и y. Требуется установить зависимость между этими переменными. Итогом испытаний является таблица:
| x | x 1 | x 2 | ... | xn |
| y | y 1 | y 2 | ... | yn |
где каждому числу xi поставлено в соответствие число уi.
Допустим, что точки, взятые из таблицы, группируются около некоторой прямой линии. Тогда можно предположить, что между x и y существует линейная зависимость 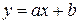 .
.
Признаком наилучшей прямой считается минимум суммы квадратов отклонений, который рассчитывается по формуле
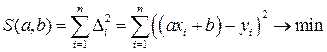
Пусть теперь точки на графике располагаются вблизи некоторой параболы так, что между x и y можно предположить квадратичную зависимость: 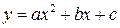 , тогда
, тогда 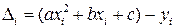 . Сумма квадратов отклонений рассчитывается по формуле
. Сумма квадратов отклонений рассчитывается по формуле
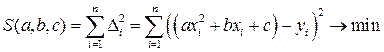
 2015-03-07
2015-03-07 268
268







