Образец выполнения. Пример 1. Решить уравнение методом хорд с точностью

Пример 1. Решить уравнение 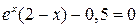методом хорд с точностью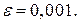

Решение.

1. Построим график функции и найдем точки пересечения его с осью Ox.

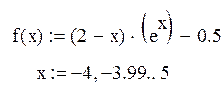
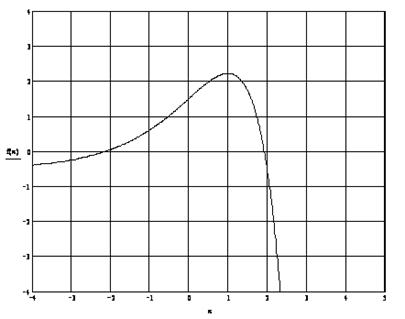
Получили два интервала [–3;–2], [1,5;2,5]. Интервал, в котором мы будем уточнять корень – [1,5;2,5].

2. Уточняем корни. Находим первую производную функции
f (x)= :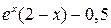

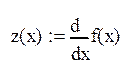
3. Определяем знаки функции f(x) на отрезке [1,5;2,5].

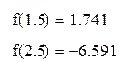
На данном отрезке действительно существует корень нашего уравнения.

4. Строим последовательность значений с использованием рекуррентной формулы метода хорд

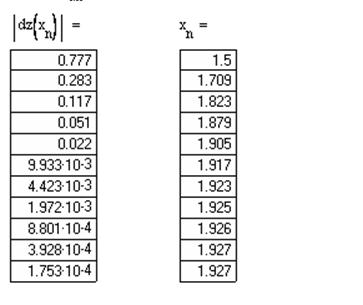
Начиная с n =8, значения x_n удовлетворяют критерию достижения заданной точности, значит, x ₈=1,927 является решением данного уравнения.

Пример 2. Вычислить методом касательных корень уравнения 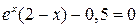на отрезке [1,5;2,5] с точностью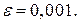

Решение.

1. Отделяем корни уравнения.

2. Определяем неподвижную точку. Для этого определяем знаки функции и второй производной на отделенном интервале [1,5; 2,5]. Для этого составим функцию, проверяющую условие неподвижности точки

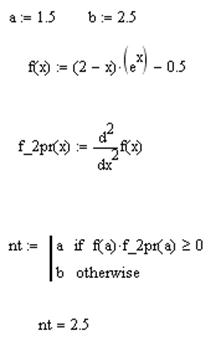
Тогда подвижной точкой будет точка a =1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных

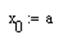
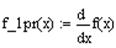
Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение x ₄=1,927 при n =4, т.к. 2,367×10^-5<0,001.

4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).

5. Проверяем полученные результаты.

Пример 3. Решить уравнение 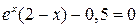методом простой итерации с точностью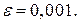

Решение:

1. Отделяем корни уравнения.

2. Приводим исходное уравнение к виду x = f (x). Заменим уравнение 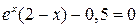уравнением вида f (x)= x-mF (x). Здесь величина m должна быть подобрана так, чтобы для функции f (x) выполнялись условия теоремы о достаточном условии сходимости итерационного процесса. Производная 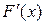на отрезке [1,5;2,5] отрицательна, следовательно, функция F (x) на этом отрезке монотонно убывает. Ее значения представлены

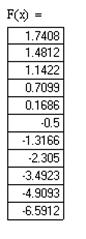
3. Тогда значения функции f (x) будут равны: 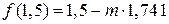и .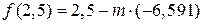

Поскольку производная 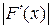на концах интервала [1,5;2,5] положительна (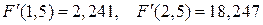) и монотонно возрастает, ее модуль имеет максимум на правом конце отрезка.

Найдем производную преобразованной функции и ее значения на концах отрезка [1,5;2,5].

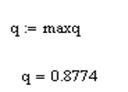
3. Вычисляем значения итерационной последовательности x_n = f (x_{n -1}).В качестве начального приближения возьмем, например, начало отрезка, точку x ₀=1,5.

Критерием достижения заданной точности при решении уравнения методом простой итерации является величина A, равная

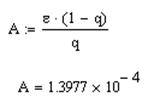
4. Строим итерационную последовательность.

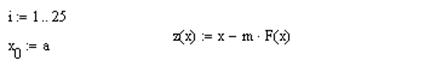
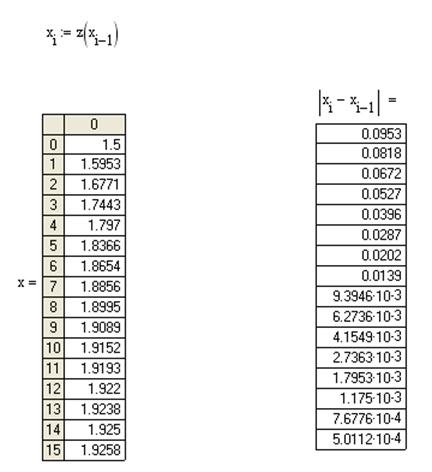
Для 24 приближения получили, что | x₂₃ – x_{2 4}|<1,398×10^-5<A. Отсюда следует, что x ₂₃=1,92718 является приближенным решением нашего уравнения.

ВАРИАНТЫ ЗАДАНИЙ

1. Отделить корни трансцендентного уравнения графически.

2. Решить уравнение методами итераций, секущих и касательных с точностью 0,001.

3. Провести сравнительную характеристику методов.

№ варианта	Задание	№ варианта	Задание

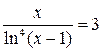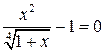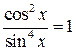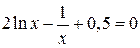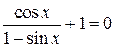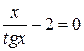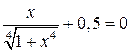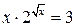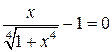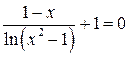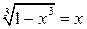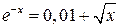СПИСОК ЛИТЕРАТУРЫ

1. Карманов Ф.И. Статистические методы обработки экспериментальных данных. Лабораторный практикум с использованием пакета MathCad. Учебное пособие / Ф.И. Карманов, В.А. Острейковский. – М: Абрис, 2012.

2. Охорзин В.А. Математическая экономика. Учебник / В.А. Охорзин. – М: Абрис, 2012.

3. Ильченко А.Н. Практикум по экономико-математическим методам / А.Н. Ильченко, О.Л. Ксенофонтова, Г.В. Канакина. – M.: Финансы и статистика, 2009.

4. Ракитин В.И. Руководство по методам вычислений и приложения MATHCAD / В.И. Ракитин. – М.: Физматлит, 2005.

5. Плис А.И. Mathcad. Математический практикум для инженеров и экономистов: учеб. пособие / А.И. Плис, Н.А. Сливина. – М.: Финансы и статистика, 2003.