Если в уравнении (1.9) правая часть равна нулю, то уравнение называется однородным. Оно имеет вид:
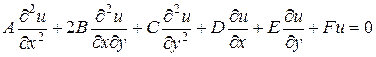 . (1.18)
. (1.18)
Вообще в теории дифференциальных уравнений уравнение называется однородным, если функция, тождественно равная нулю (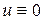 ), является его решением. Решения линейных однородных уравнений вида (1.18) обладают следующими свойствами:
), является его решением. Решения линейных однородных уравнений вида (1.18) обладают следующими свойствами:
1) если 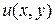 есть решение линейного однородного уравнения (1.18), то
есть решение линейного однородного уравнения (1.18), то 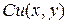 , где
, где 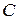 – любая постоянная, есть также решение уравнения (1.18);
– любая постоянная, есть также решение уравнения (1.18);
2) если 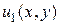 и
и 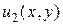 – решение линейного однородного уравнения (1.18), то сумма
– решение линейного однородного уравнения (1.18), то сумма 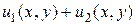 есть также решение этого уравнения;
есть также решение этого уравнения;
3) если каждая из функций 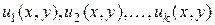 является решением уравнения (1.18), то и их линейная комбинация:
является решением уравнения (1.18), то и их линейная комбинация:
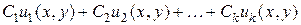 , (1.19)
, (1.19)
где 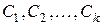 – произвольные постоянные, также является решением этого уравнения.
– произвольные постоянные, также является решением этого уравнения.
Для доказательства достаточно заметить, что если и есть линейная комбинация частных решений: 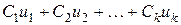 , то любая производная функции
, то любая производная функции 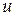 будет такой же линейной комбинацией соответствующих производных функций
будет такой же линейной комбинацией соответствующих производных функций 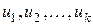 :
:
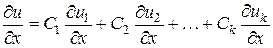 ;
; 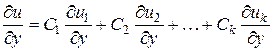 .
.
Разумеется, также будут выглядеть и производные второго порядка. Если подставить выражения для производных функций в левую часть уравнения (1.18) и перегруппировать слагаемые, то получим:
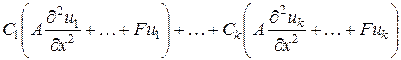 .
.
Поскольку по условию функции 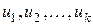 являются решениями уравнения (1.18), то каждая из скобок обратится в нуль, а вместе с ними и вся левая часть уравнения. Это и означает, что функция
являются решениями уравнения (1.18), то каждая из скобок обратится в нуль, а вместе с ними и вся левая часть уравнения. Это и означает, что функция 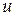 является его решением.
является его решением.
Уравнение в частных производных может иметь бесконечное множество линейно независимых частных решений, т.е. такое множество решений, любое конечное число которых являются функциями линейно независимыми.
Система функций 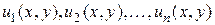 , называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных.
, называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных.
В соответствии с этим будем иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами, членами которых служат произведения произвольных постоянных на частные решения:
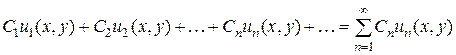 . (1.20)
. (1.20)
4. Основные типы уравнений математической физики
К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.
4.1. Волновое уравнение:
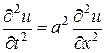 . (1.21)
. (1.21)
Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т.д.
4.2. Уравнение теплопроводности, или уравнение Фурье:
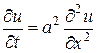 . (1.22)
. (1.22)
Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т.д.
4.3. Уравнение Лапласа:
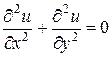 , (1.23)
, (1.23)
или в операторной форме:
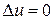 , (1.24)
, (1.24)
где 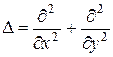 – оператор Лапласа.
– оператор Лапласа.
Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т.д.
4.4. Уравнение Пуассона:
в общем случае в векторной форме уравнение имеет вид:
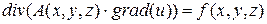 , (1.25)
, (1.25)
где 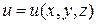 – искомая функция;
– искомая функция; 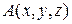 ,
, 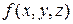 – некоторые функции независимых переменных.
– некоторые функции независимых переменных.
Данное уравнение может быть записано в частных производных, если учесть, что по определению градиент некоторого скалярного поля 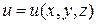 определяется выражением:
определяется выражением:
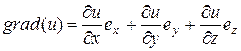 , (1.26)
, (1.26)
где 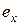 ,
, 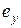 ,
, 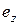 – единичные вектора (орты) в направлениях соответствующих координатных осей, а дивергенция некоторого векторного поля
– единичные вектора (орты) в направлениях соответствующих координатных осей, а дивергенция некоторого векторного поля 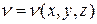 – выражением:
– выражением:
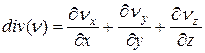 , (1.27)
, (1.27)
где 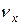 ,
, 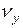 ,
, 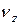 – проекции вектора
– проекции вектора 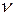 на соответствующие оси координат.
на соответствующие оси координат.
Таким образом, получим:
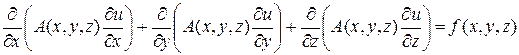 , (1.28)
, (1.28)
или в операторной форме:
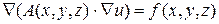 , (1.29)
, (1.29)
где 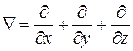 – оператор Наббла.
– оператор Наббла.
Из полученных выражений видно, что уравнение Пуассона является обобщенным уравнением Лапласа для случая отличной от нуля правой части.
 2015-03-07
2015-03-07 1470
1470
