Граничные условия

Предположим, необходимо решить определенную задачу, описываемую уравнениями математической физики, для некоторой области 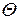. Тогда для нахождения единственного решения необходимо задать граничные условия (ГУ), т.е. выразить искомые переменные на границе 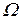области 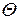некоторыми уравнениями.

Если область 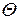представляет собой некоторый объем в трехмерном пространстве, то граница 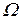будет представлять собой замкнутую поверхность в этом пространстве, ограничивающую заданный объем. Если область 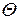представляет собой некоторую поверхность в двухмерном пространстве, то граница 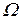будет представлять собой замкнутый контур в этом пространстве, ограничивающий заданную поверхность. И, наконец, если область 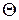представляет собой некоторый отрезок в одномерном пространстве, то граница 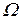будет представлять собой две точки на границах заданного отрезка.

По виду уравнений, задающих ГУ, различают граничные условия первого рода (условия Дирихле), второго рода (условия Неймана) и третьего рода.

Граничные условия первого рода или краевая задача Дирихле имеют вид:

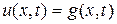при , ,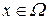

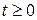где 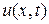– искомая функция; 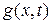– некоторая заданная функция на границе 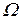функция; 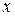– координаты граничной точки в пространстве (например, для трехмерного пространства 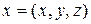); 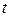– время.

Для задачи теплопроводности ГУ первого рода задают температуру на границе 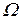. В задаче о распределении электростатического поля в непроводящей среде ГУ первого рода задают электрический потенциал на границе 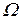и т.д.

Граничные условия второго рода или краевая задача Неймана имеют вид:

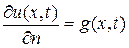при , ,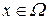

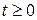где 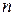– внутренняя нормаль к границе .

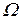Иными словами, условия Неймана задают поток на границе, точнее, проекцию вектора потока на внутреннюю нормаль к границе. Например, в задачах теплопроводности ГУ второго рода задают тепловой поток, в задаче о распределении электростатического поля в непроводящей среде – проекцию вектора напряженности электрического поля на нормаль к границе и т.д.

Граничные условия третьего рода являются более общим случаем краевых задач Дирихле и Неймана и имеют вид:

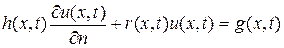при , ,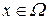

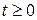где 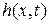, 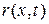– некоторые функции координат и времени.

Например, в тепловых задачах ГУ третьего рода используют для задания на границе конвективного и излучательного теплообмена.

Следует отметить, что количество граничных условий для каждой переменной определяется максимальным порядком производных по координатам в дифференциальных уравнениях: для уравнений первого порядка – одно ГУ, для уравнений второго порядка – два, для уравнений третьего порядка – три ГУ и т.д.