2015-03-07
1328
Для нахождения единственного решения в задачах, описывающих нестационарные, т.е. изменяющиеся во времени физические процессы, помимо граничных необходимо задавать еще и начальные условия, определяющие значения переменных или их градиентов во всех внутренних точках рассматриваемой области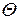 
, исключая границу 
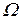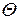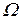( \ ), в начальный момент времени:
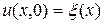при 
;
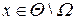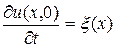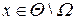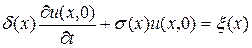при ;
при ,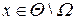
где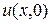 
– искомая функция в начальный момент времени; 
, 
, 
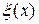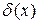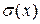– некоторые функции координат.
Аналогично граничным условиям, количество начальных условий для каждой переменной определяется максимальным порядком производной по времени в дифференциальных уравнениях.
Различают три основных типа задач для дифференциальных уравнений с частными производными:
a) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, граничные условия отсутствуют;
b) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе области, начальные условия отсутствуют;
c) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия.
