(методом Фурье)
Метод разделения переменных применяется для решения многих задач математической физики. Пусть требуется найти решение волнового уравнения
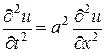 , (2.26)
, (2.26)
удовлетворяющее граничным условиям
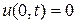 ,
, 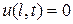 , (2.27), (2.28)
, (2.27), (2.28)
и начальным условиям
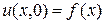 ,
, 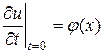 . (2.29),(2.30)
. (2.29),(2.30)
Частное решение уравнения (2.26), удовлетворяющее граничным условиям (2.27) и (2.28), ищут в виде произведения двух функций:
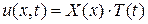 .
.
Подставляя функцию 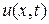 в уравнение (2.26) и преобразовывая его, получим:
в уравнение (2.26) и преобразовывая его, получим:
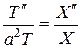 .
.
В левой части этого уравнения стоит функция, которая не зависит от 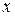 , а в правой – функция, не зависящая от
, а в правой – функция, не зависящая от 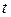 . Равенство возможно только в том случае, когда левая и правая части не зависят ни от
. Равенство возможно только в том случае, когда левая и правая части не зависят ни от 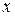 , ни от
, ни от 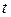 , т.е. равны постоянному числу. Обозначим
, т.е. равны постоянному числу. Обозначим
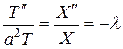 , где
, где 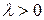 . (2.31)
. (2.31)
Из этих уравнений получаем два однородных дифференциальных уравнения второго порядка с постоянными коэффициентами:
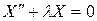 , (2.32)
, (2.32)
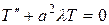 . (2.33)
. (2.33)
Общее решение этих уравнений
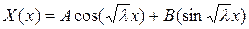 , (2.34)
, (2.34)
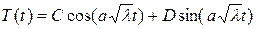 , (2.35)
, (2.35)
где 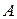 ,
, 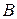 ,
, 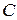 ,
, 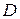 – произвольные постоянные.
– произвольные постоянные.
Постоянные 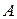 и
и 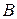 подбирают так, чтобы выполнялись условия (2.27) и (2.28), из которых следует, что
подбирают так, чтобы выполнялись условия (2.27) и (2.28), из которых следует, что 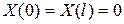 , так как
, так как 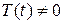 (в противном случае
(в противном случае 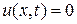 ). Подставляя значения
). Подставляя значения 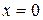 и
и 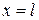 в равенство (2.34), на основании (2.27) и (2.28) получаем
в равенство (2.34), на основании (2.27) и (2.28) получаем 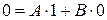 ,
, 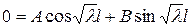 . Откуда находим:
. Откуда находим:
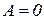 и
и 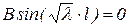 .
.
Так как 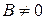 (иначе, было бы
(иначе, было бы 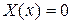 и
и 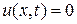 , что противоречит условию), то должно выполняться равенство:
, что противоречит условию), то должно выполняться равенство: 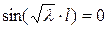 ,
, 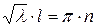 ,
,
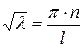 ,
, 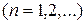 (2.36)
(2.36)
откуда,
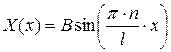 . (2.37)
. (2.37)
Найденные значения 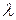 называют собственными значениями для данной краевой задачи. Соответствующие им функции
называют собственными значениями для данной краевой задачи. Соответствующие им функции 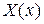 называются собственными функциями. Вид собственных значений и собственных функций зависит от вида граничных условий задачи (см. Приложение №1).
называются собственными функциями. Вид собственных значений и собственных функций зависит от вида граничных условий задачи (см. Приложение №1).
Заметим, что, если в равенстве (2.31) вместо 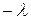 взять число
взять число 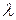
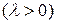 , то уравнение (2.32) будет иметь решение в виде:
, то уравнение (2.32) будет иметь решение в виде:
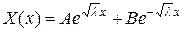 .
.
Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (2.27) и (2.28).
Полученное значение 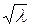 подставляем в уравнение (2.35), получим:
подставляем в уравнение (2.35), получим:
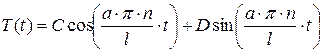 ,
, 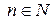 . (2.38)
. (2.38)
Для каждого значения 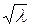 , а, следовательно, для каждого значения
, а, следовательно, для каждого значения 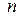 получаем решение уравнения (2.26):
получаем решение уравнения (2.26):
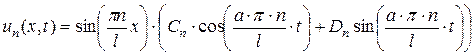 . (2.39)
. (2.39)
Так как исходное уравнение (2.26) линейное и однородное, то сумма решений также является решением уравнения, и потому функция:
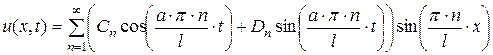 (2.40)
(2.40)
будет решением дифференциального уравнения (2.26), удовлетворяющим граничным условиям (2.27) и (2.28).
Найденное частное решение (2.40) должно еще удовлетворять начальным условиям (2.29) и (2.30). Из условия (2.29), подставляя в (2.40) значение 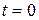 получим
получим
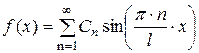 . (2.41)
. (2.41)
Далее, дифференцируя члены ряда (2.40) по переменной 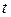 , согласно (2.30) будем иметь
, согласно (2.30) будем иметь
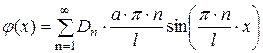 . (2.42)
. (2.42)
Правые части равенств (2.41) и (2.42) есть ряды Фурье для функций 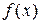 и
и 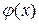 , разложенных по синусам на интервале
, разложенных по синусам на интервале 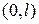 . Поэтому
. Поэтому
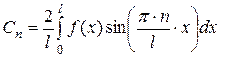 , (2.43)
, (2.43)
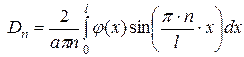 . (2.44)
. (2.44)
В зависимости от вида функций начальных и граничных условий могут получаться различные виды разложений заданных функций в ряд Фурье (см. Приложение №2).
Итак, ряд (2.40), для которого коэффициенты 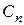 и
и 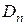 определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (2.26), удовлетворяющее граничным и начальным условиям (2.27 – 2.30).
определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (2.26), удовлетворяющее граничным и начальным условиям (2.27 – 2.30).
Пример. Найти решение уравнения:
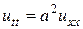 ,
, 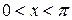 ,
, 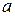 =2, (2.45)
=2, (2.45)
удовлетворяющее краевым условиям:
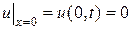 , (2.46)
, (2.46)
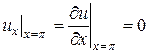 , (2.47)
, (2.47)
и начальным условиям:
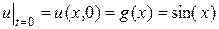 , (2.48)
, (2.48)
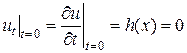 . (2.49)
. (2.49)
Будем искать (не равное тождественно нулю) частное решение уравнения (2.45), удовлетворяющее граничным условиям (2.46) и (2.47), в виде произведения двух функций 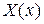 и
и 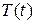 , из которых первая зависит только от
, из которых первая зависит только от 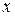 , а вторая только от
, а вторая только от 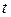 :
:
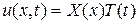 . (2.50)
. (2.50)
Общие решения для функций 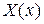 и
и 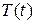 будут:
будут:
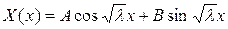 , (2.51)
, (2.51)
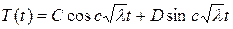 , (2.52)
, (2.52)
где 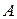 ,
, 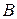 ,
, 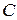 ,
, 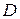 – произвольные постоянные.
– произвольные постоянные.
Подберем постоянные 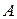 и
и 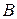 так, чтобы удовлетворялись условия (2.46) и (2.47). Так как
так, чтобы удовлетворялись условия (2.46) и (2.47). Так как 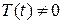 (в противном случае будет
(в противном случае будет 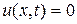 , что противоречит поставленному условию), то функция
, что противоречит поставленному условию), то функция 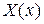 должна удовлетворять условиям (2.46) и (2.47), т.е. должно быть
должна удовлетворять условиям (2.46) и (2.47), т.е. должно быть 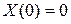 ,
, 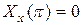 . Подставляя значение
. Подставляя значение 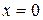 в равенство (2.51), на основании (2.46) получаем
в равенство (2.51), на основании (2.46) получаем 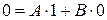 . Из этого уравнения находим
. Из этого уравнения находим 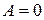 .
.
Для проверки условия (2.47) найдем производную функции 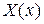 и подставим туда значение
и подставим туда значение 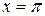 :
:
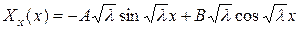 ,
,
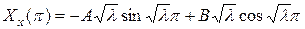 .
.
Из последнего уравнения следует 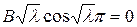 .
. 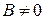 , т.к. в противном случае было бы
, т.к. в противном случае было бы 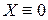 и
и 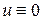 , что противоречит условию,
, что противоречит условию, 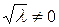 , т.к. уравнение теряет смысл (все обращается в нуль). Следовательно, должно быть
, т.к. уравнение теряет смысл (все обращается в нуль). Следовательно, должно быть 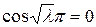 , откуда
, откуда 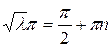 , (
, (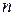 =0,1,…). Получили:
=0,1,…). Получили:
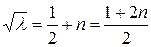 , (
, (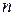 =0,1,…). (2.53)
=0,1,…). (2.53)
Итак, мы получили:
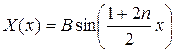 . (2.54)
. (2.54)
Зная 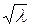 , пользуясь равенством (2.52), можем записать:
, пользуясь равенством (2.52), можем записать:
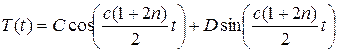 , (
, (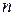 =0,1,…).
=0,1,…).
Подставим 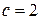 в последнее уравнение, упростим и получим:
в последнее уравнение, упростим и получим:
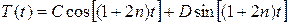 . (2.55)
. (2.55)
Для каждого значения 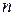 , следовательно для каждого
, следовательно для каждого 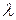 , выражения (2.54) и (2.55) подставляем в равенство (2.50) и получаем решение уравнения (2.45), удовлетворяющее граничным условиям (2.46) и (2.47). Это решение обозначим
, выражения (2.54) и (2.55) подставляем в равенство (2.50) и получаем решение уравнения (2.45), удовлетворяющее граничным условиям (2.46) и (2.47). Это решение обозначим 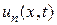 :
:
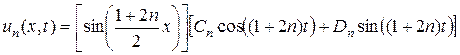 .
.
Так как уравнение (2.45) линейное и однородное, то сумма решений также является решением, и потому функция, представленная рядом:
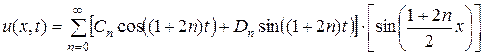 (2.56)
(2.56)
также будет решением дифференциального уравнения (2.45), которое будет удовлетворять граничным условиям (2.46) и (2.47).
Решение (2.56) должно еще удовлетворять начальным условиям (2.48) и (2.49). Этого мы будем добиваться путем подбора постоянных 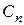 и
и 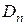 . Подставляя в равенство (2.56)
. Подставляя в равенство (2.56) 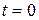 (см. условие (2.48)), получим
(см. условие (2.48)), получим
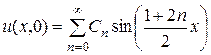 :
:
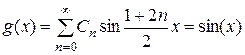 . (2.57)
. (2.57)
Из последнего равенства получим:
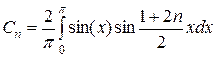 . (2.58)
. (2.58)
Преобразуем подынтегральное выражение:
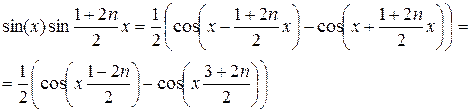
Найдем постоянную 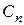 :
:
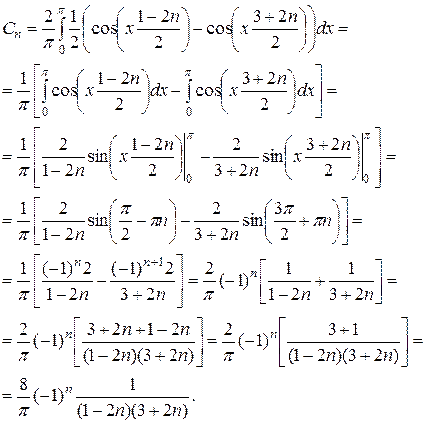
Далее, дифференцируем члены равенства (2.56) по 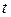 и подставляем
и подставляем 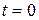 :
:
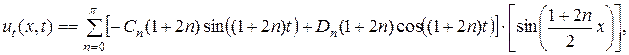
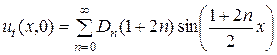 .
.
Из условия (2.49) получается равенство:
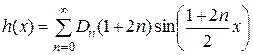 . (2.59)
. (2.59)
Определяем коэффициенты Фурье этого ряда:
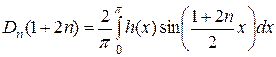
или
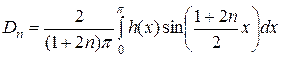 . (2.60)
. (2.60)
Так как 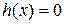 , получаем, что коэффициент
, получаем, что коэффициент 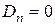 .
.
Итак, получили частное решение в виде:
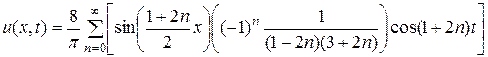 , (2.61)
, (2.61)
которое является решением уравнения (2.45) и удовлетворяет граничным и начальным условиям (2.46) – (2.49).
 2015-03-07
2015-03-07 3215
3215
