2015-03-07
2986
Для выделения единственного решения уравнения теплопроводности необходимо к уравнению присоединить начальные и граничные условия.
Начальное условие, в отличие от уравнения гиперболического типа состоит лишь в задании значений функции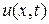 
в начальный момент времени 
.
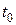Граничные условия могут быть различны в зависимости от температурного режима на границах. Рассматривают три основных типа граничных условий.
1. На концах стержня задана температура:
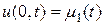, (3.20)
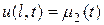, (3.21)
где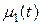 
, 
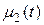– функции, заданные в некотором промежутке времени 
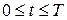, в течение которого изучается процесс.
2. На концах стержня заданы значения производной:
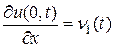, (3.22)
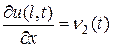. (3.23)
К этому условию мы приходим, если задана величина теплового потока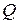 
, протекающего через торцевое сечение стержня. Например, если для 
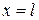задана величина 
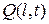, то:
,
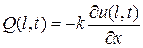откуда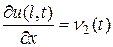 
, где 
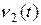– известная функция, выражающаяся через заданный поток 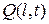формулой 
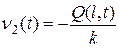. Ес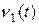ли 
или 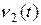тождественно равны нулю, то говорят, что соответствующий конец стержня теплоизолирован.
3. На концах стержня заданы линейные отношения между функцией и ее производной:
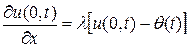, (3.24)
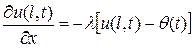, (3.25)
где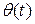 
– известная функция – температура окружающей среды; 
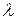– коэффициент теплообмена. Это граничное условие соответствует теплообмену по закону Ньютона на поверхности тела с окружающей средой, температура которой 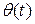известна.
Пользуясь двумя выражениями для теплового потока, вытекающего через сечение :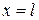
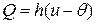
и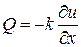 
,
получаем математическую формулировку третьего граничного условия в ви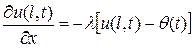де:
, где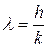 
.
Для конца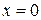 
стержня 
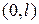третье граничное условие имеет вид:
.
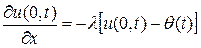Граничные условия пр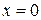и и 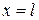могут быть различных типов, так что число различных задач велико.
Первая краевая задача для ограниченного стержня состоит в следующем.
Найти решение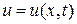 
уравнения теплопроводности:
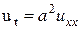при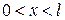 
, 
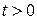, (3.26)
удовлетворяющее условиям:
, 
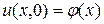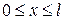, (3.27)
, , 
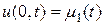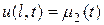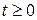, (3.28), (3.29)
где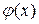 
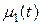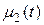, , – заданные функции.
Физически условие 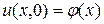(начальное условие) соответствует тому, что при 
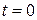в различных сечениях стержня задана температура, равная 
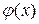. Условия 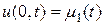, 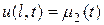(граничные условия) соответствуют тому, что на концах стержня пр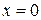и и 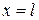поддерживается температура, равная 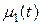и 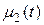соответственно.
Т.е., как и для уравнений гиперболического типа, функция 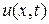ищется только для 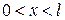и 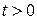(но не пр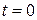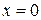и , и 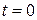, , 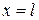где значения функции 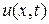заранее задаются начальными и граничными условиями).
