Формула Даламбера решения задачи Коши для волнового уравнения

Прежде чем решать задачу о колебаниях закрепленной струны, рассмотрим более простую задачу – о колебаниях бесконечной струны. Если представить очень длинную струну, то ясно, что на колебания, возникающие в ее средней части, концы струны не будут оказывать заметного влияния.

Рассматривая свободные колебания, необходимо решить однородное уравнение:

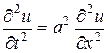(2.8)

при начальных условиях

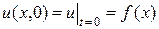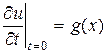, , (2.9)

где функци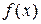и и 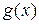заданы на всей числовой оси. Такая задача называется задачей с начальными условиями или задачей Коши.

Преобразуем волновое уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик:

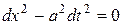
распадается на два уравнения:

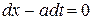и ,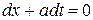

интегралами которых служат прямые:

, .

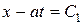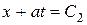Введем новые переменные 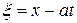, 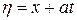и запишем волновое уравнение для переменных 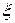и .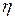

Вычисляя производные

, ,

,

,

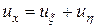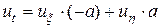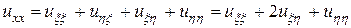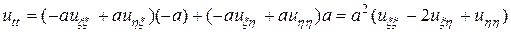и подставляя их в исходное уравнение, видим, что уравнение колебания струны в новых координатах будет:

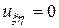. (2.10)

Интегрируя полученное равенство по 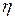при фиксированном 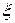, придем к равенству 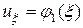. Интегрируя это равенство по 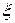при фиксированном 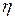, получим:

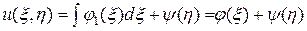, (2.11)

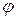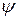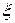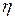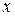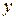где и являются функциями только переменных и соответственно. Следовательно, переходя к переменным и , получим общее решение уравнения (2.8):

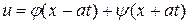. (2.12)

Найдем функци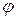и и 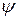так, чтобы удовлетворялись начальные условия (2.9):

.

,

.

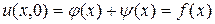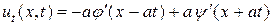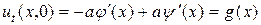Интегрируя последнее равенство, получим:

,

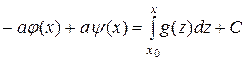где 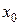и 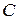– произвольные постоянные. Из системы уравнений:

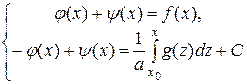
находим

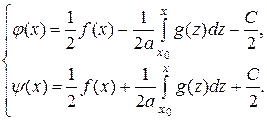(2.13)

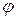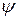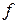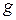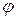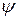Таким образом, мы определили функции и через заданные функции и , причем полученные равенства должны иметь место для любого значения аргумента. Подставляя в (2.8) найденные значения и , получим:

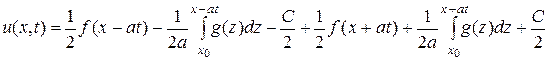
или

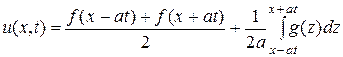. (2.14)

Найденное решение (2.14) уравнения (2.8) с начальными условиями (2.9) называется формулой Даламбера решения задачи Коши для волнового уравнения.