2015-03-07
1333
Рассмотрим в качестве примера нестационарное уравнение теплопроводности, которое получается на основании закона Фурье, согласно которому вектор плотности теплового потока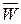 
пропорционален градиенту температуры 
:
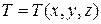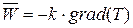, (3.1)
где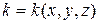 
– коэффициент теплопроводности.
Плотность теплового потока равна количеству теплоты, протекающему в единицу времени через единичную площадь изотермической поверхности.
Рассмотрим задачу о нестационарном распределении тепла в некотором объеме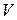 
, ограниченном замкнутой поверхностью 
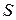трехмерного пространства 
.
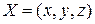Количество тепла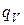 
, выделившегося в объеме 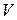, ограниченного поверхностью 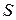, за некоторый промежуток времени 
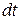, можно определить как
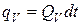, (3.2)
где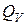 
– суммарное количество тепла, выделяющегося в единицу времени в объеме 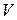, ограниченном поверхностью 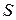, определяемое интегралом:
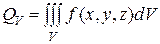, (3.3)
где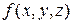 
– известное распределение плотности источников тепла.
Учитывая, что рассматривается неравновесное состояние системы, часть тепла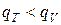 
идет на изменение во времени температуры в объеме 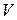и определяется выражением:
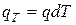, (3.4)
где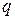 
– суммарное количество тепла, необходимого для изменения температуры объема 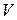на один градус; 
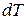– изменение температуры объема 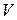за промежуток времени .
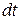Остальная часть тепла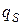 
протекает через ограничивающую поверхность площадью :
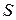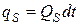, (3.5)
где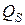 
– суммарное количество тепла, протекающего в единицу времени через поверхность 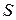, определяемое интегралом:
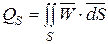, (3.6)
где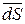 
– вектор, модуль которого численно равен площади 
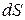соответствующего бесконечно малого элемента поверхности, а направление совпадает с направлением нормали к этому элементу; 
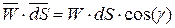– скалярное произведение векторов 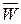и ;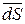 
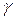– угол между ними.
Иными словами, в нестационарном случае должно быть справедливо уравнение:
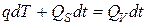. (3.7)
Учитывая, что в общем случае неоднородной среды суммарное количество тепла 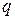, необходимое для изменения температуры объема 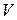на один градус определяется выражением:
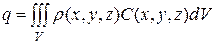, (3.8)
где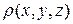 
– плотность вещества; 
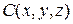– удельная теплоемкость вещества, подставляя выражения (3.3), (3.6), (3.8) в уравнение (3.7) и применяя теорему Остроградского-Гаусса 
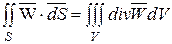, получим:
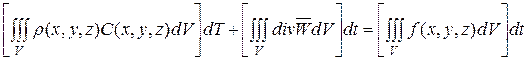, (3.9)
откуда, вынося подынтегральные выражения, разделив левую и правую части на 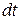и подставляя закон Фурье (3.1), можем записать нестационарное уравнение теплопроводности в векторной форме:
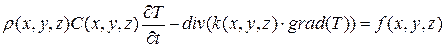. (3.10)
В операторной форме уравнение (10) имеет вид:
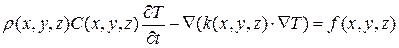. (3.11)
