Разбиваем механизм на три составляющие. Первый механизм, состоящий из колес 1 и 2, является простым механизмом с неподвижными осями. Второй – планетарный, имеющий колеса 3, 4, 5 и водило H. У этого механизма ось колеса 4 движется в пространстве. Третий механизм с колесами 6 и 7 относится также к простым с неподвижными осями.
В планетарном механизме не дано число зубьев колеса 5. Для его нахождения используем условие соосности, которое говорит о том, что оси колес 3 и 5 располагаются на одной прямой (колеса соосны) и расстояние A равно радиусу колеса 5 или сумме двух радиусов колеса 4 и одного радиуса колеса 3, т.е.
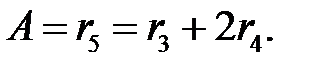
Считаем модуль колес одинаковым и равным 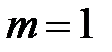 мм и, имея в виду, что
мм и, имея в виду, что 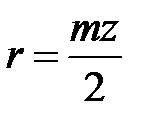 , получим
, получим
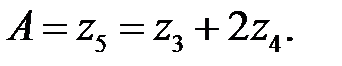
Следовательно,
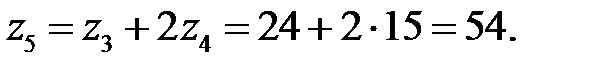
Находим передаточное отношение всего механизма
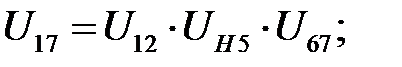
где 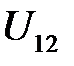 – передаточное отношение первого механизма,
– передаточное отношение первого механизма,
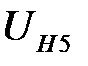 – передаточное отношение второго механизма,
– передаточное отношение второго механизма,
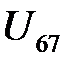 – передаточное отношение третьего механизма.
– передаточное отношение третьего механизма.
Отношение 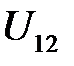 находим через числа зубьев
находим через числа зубьев
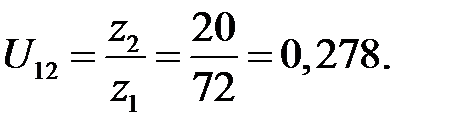
Так как колеса имеют внутреннее зацепление и они вращаются в одну сторону, то отношение имеет знак «плюс».
Передаточное отношение 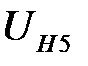 планетарного механизма определяем, используя формулу Виллиса
планетарного механизма определяем, используя формулу Виллиса
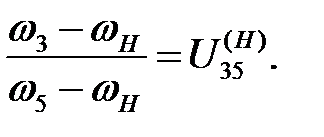
Здесь 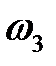 – угловая скорость входного центрального колеса 3,
– угловая скорость входного центрального колеса 3,
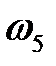 – угловая скорость выходного центрального колеса 5,
– угловая скорость выходного центрального колеса 5,
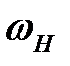 – угловая скорость водила H,
– угловая скорость водила H,
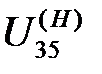 – передаточное отношение от колеса 3 к колесу 5 при остановленном водиле H.
– передаточное отношение от колеса 3 к колесу 5 при остановленном водиле H.
В данном случае имеем
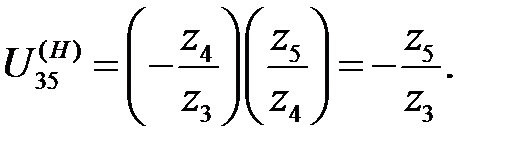
Передаточное отношение в первых скобках отрицательно, т.к. колеса 3 и 4 имеют внешнее зацепление, а у колес 4 и 5 зацепление внутреннее. Разделим числитель и знаменатель в формуле Виллиса на 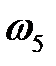
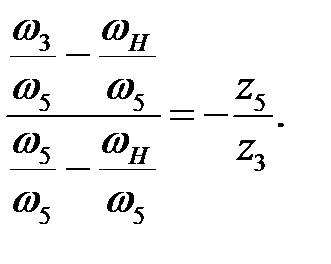
Так как 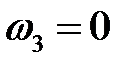 и
и 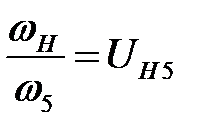 , то получим
, то получим
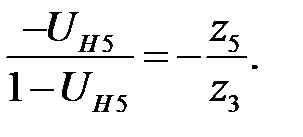
Отсюда окончательно найдем 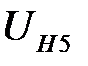
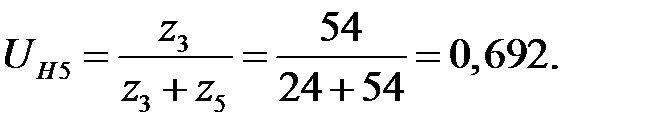
Положительное значение 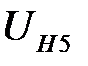 свидетельствует о том, что водило H и колесо 5 вращаются в одну сторону.
свидетельствует о том, что водило H и колесо 5 вращаются в одну сторону.
Передаточное отношение третьего механизма
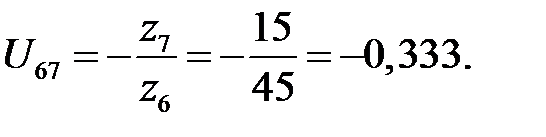
Это отношение отрицательно, так как колеса 6 и 7 имеют внешнее зацепление.
Находим передаточное отношение всего механизма
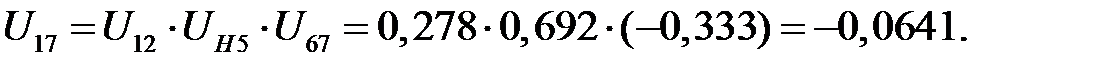
Так как 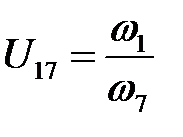 , то будем иметь
, то будем иметь
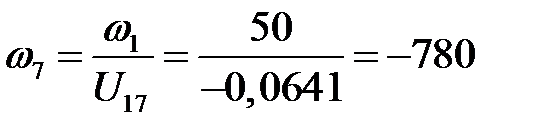 1/c.
1/c.
Отрицательная величина скорости 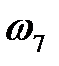 говорит о том, что колеса 1 и 7 вращаются в разные стороны.
говорит о том, что колеса 1 и 7 вращаются в разные стороны.
 2015-03-07
2015-03-07 607
607








