2015-03-07
472
На листе № 4 курсового проекта изображаем схему механизма в масштабе. Для этого находим диаметры колес по формуле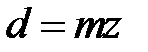 
. Так как 
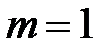мм, то получим: 
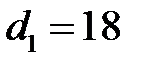мм, 
мм,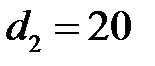 
мм, 
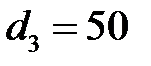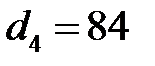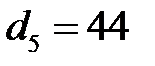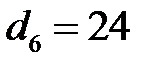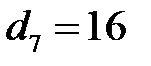мм, 
мм,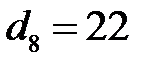 
мм, 
мм,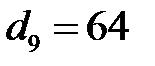 
мм, 
мм.
Принимаем масштаб М1:1, что соответствует масштабному коэффициенту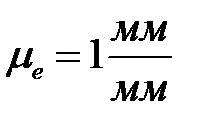 
, т.е. механизм изображается в натуральную величину.
Обозначаем оси неподвижных колес через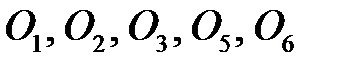 
(рис. 5.1). Подвижную ось сателлита 5-6 обозначим 
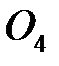. Места зацепления колес обозначаем заглавными буквами 
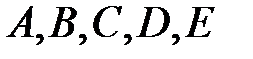. Справа от схемы механизма проводим вертикальную линию 
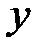, на которую сносим неподвижные оси, обозначая полученные точки строчными буквами 
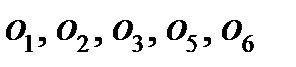. На эту же линию сносим точку D неподвижного колеса 7, получая точку d.
На горизонтальной линии, проходящей через зацепление A от вертикали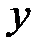 
откладываем в ту или другую сторону произвольный отрезок 
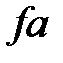, изображающий скорость точки A. Затем соединяем точки a и 
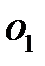, получая линию распределения скоростей колеса 1. Линия скоростей колеса 2 проходит через точки a и 
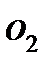. На продолжении этой прямой лежит точка b. Так как зацепления B и C принадлежат одному сдвоенному колесу 3-4, то соединяя точки b и 
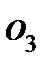, находим точку c, которая относится и к колесу 5 сателлита 5-6. Если соединить точки c и d, то получим линию скоростей сателлита, на которой будет лежать точка 
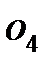водила H. Соединяем 
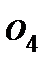с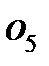 
, находим положение точки e. Линия 
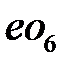представляет собой прямую скоростей выходного колеса 9.
Изображаем произвольную горизонтальную прямую x. Ниже этой прямой также произвольно выбираем точку o, из которой проводим вертикальную линию и два луча, параллельные линиям распределения скоростей колес 1 и 9. Получаем точки k, q, p. Замеряем расстояния qp и qk и находим их отношение
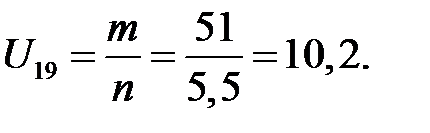
Если отрезки qp и qk располагаются от вертикали ok с одной стороны, то передаточное отношение получается положительным, а если с разных сторон, то – отрицательным. В данном случае оно положительное.
Угловая скорость колеса 9
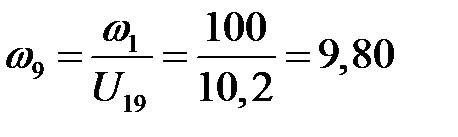1/c.
Сравнивая результаты, полученные аналитическим и графическим методами, отмечаем высокую точность вычислений и построений.
