2015-03-07
875
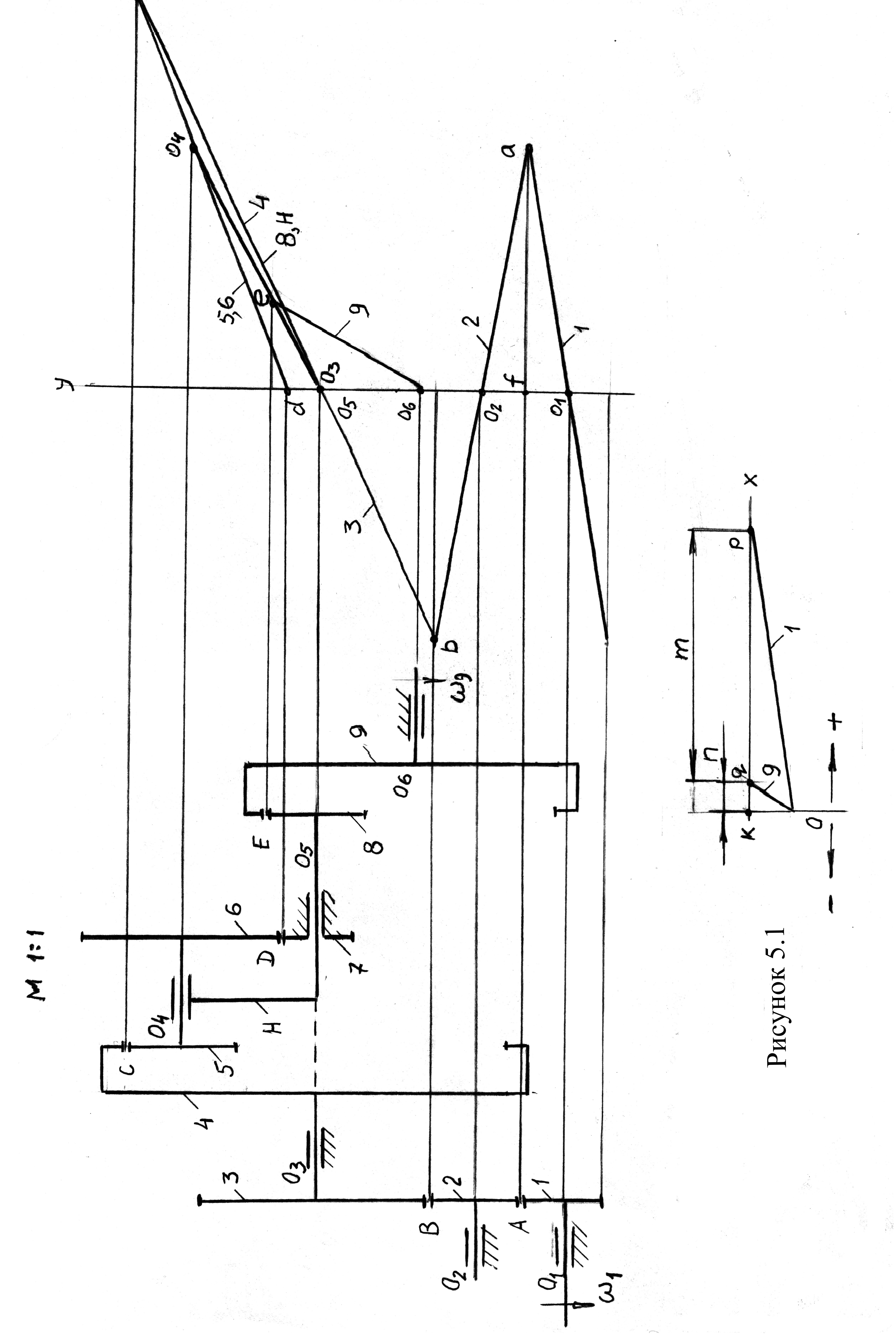
Разбиваем сложный зубчатый механизм (рис.5.1) на три составляющие. Первый механизм, состоящий из колес 1, 2, 3, является простым механизмом с неподвижными осями. Второй – планетарный, состоящий из колес 4, 5, 6, 7 и водила H. У этого механизма ось колес 5 и 6 движется в пространстве. Третий механизм, имеющий колеса 8 и 9, относится к простым с неподвижными осями.
В первом механизме не дано число зубьев колеса 2. Это колесо, называемое паразитным, не влияет на величину передаточного отношения и служит для изменения направления вращения. Принимаем число зубьев этого колеса произвольно, например,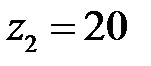 
.
У планетарного механизма не дано число зубьев колеса 6. Для его нахождения используем условие соосности, которое заключается в том, что величина А равна разности радиусов колес 4 и 5 или сумме радиусов колес 6 и 7, причем оси колес 4 и 7 расположены на одной прямой (колеса сосны). Следовательно,
.
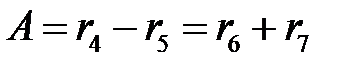Считаем модуль колес одинаковым и равным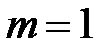 
мм, и, имея в виду, что 
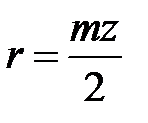, получим
.
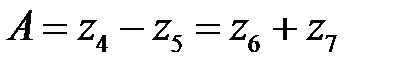Отсюда находим
.
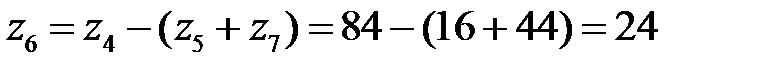Определяем передаточное отношение всего механизма, как произведение передаточных отношений отдельных составляющих механизмов
.
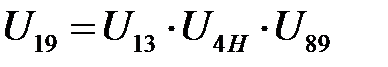Передаточное отношение первого механизма находим по числу зубьев
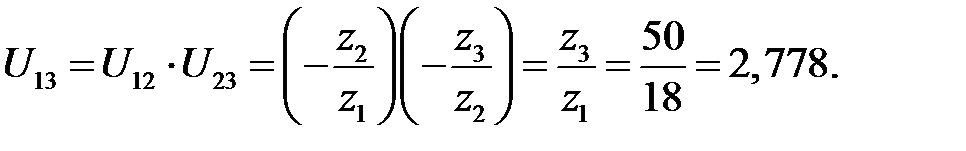
Знаки «минус» в скобках говорят о том, что колеса 1 и 2, так же, как и колеса 2 и 3, имеют внешнее зацепление. Положительная величина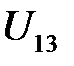 
свидетельствует о том, что колеса 1 и 3 вращаются в одну сторону.
Передаточное отношение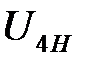 
планетарного механизма определяем, используя формулу Виллиса
,
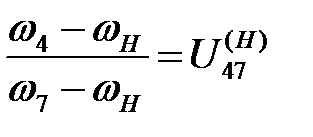где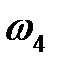 
– угловая скорость входного центрального колеса 4,
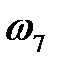– угловая скорость выходного центрального колеса 7,
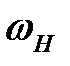– угловая скорость водила H,
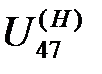– передаточное отношение от колеса 4 к колесу 7 при остановленном водиле.
В рассматриваемом примере имеем
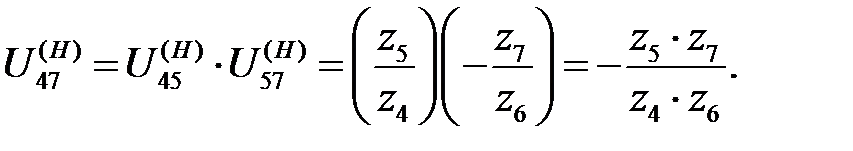
Разделим числитель и знаменатель в формуле Виллиса на 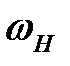, получим
.
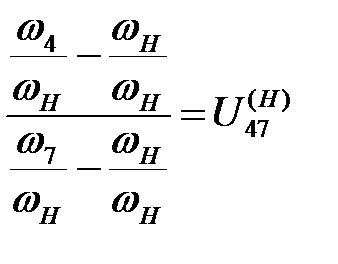Так как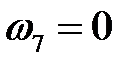 
, а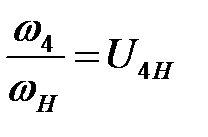 
, то будем иметь
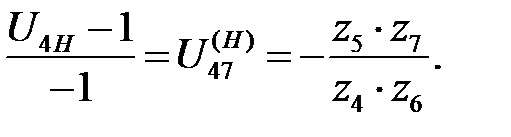
Отсюда
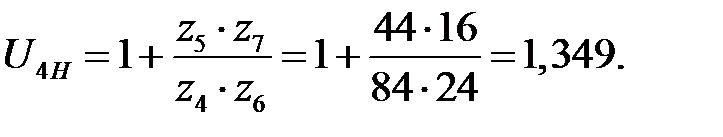
Знак «плюс» говорит о том, что колесо 4 и водило H вращаются в одном направлении.
Передаточное отношение третьего механизма
.
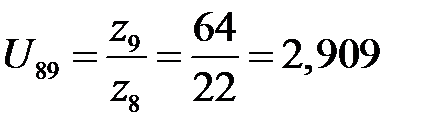Здесь отношение взято со знаком «плюс», так как колеса 8 и 9 имеют внутреннее зацепление.
Передаточное отношение всего механизма
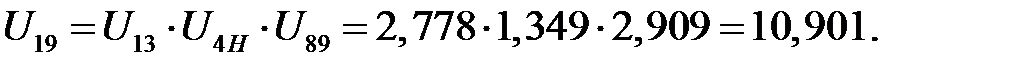
Но так как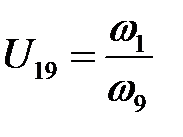 
, получим
1/с.
Так как по знаку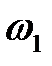 
и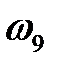 
одинаковы, то колеса 1 и 9 имеют одно направление вращения.
