2015-03-07
1759
Рассмотрим однородные уравнения теплопроводности.
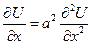
При отсутствии внешних источников тепла. Поставим задачу Коми:
Найти функцию U(x,t) удовлетворяющую уравнению:
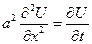
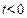
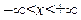
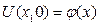
Физический смысл задачи – определение температуры однородного бесконечного стержня в любой момент времени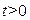 
по известн. температуре 
в начальный момент времени t=0.
Считается, что токов. поверхность стержня теплоизолирована (тепло из стержня не уходит)
Предположим теперь, что функции U(x,t) и достаточно гладкие функции, убывающие при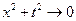 
Настолько быстро, что существ. преобразов. Фурье
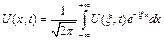преобразование Фурье функции 
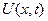по перемен. Х.
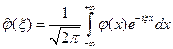
2. Законны операции дифферен.
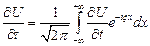и
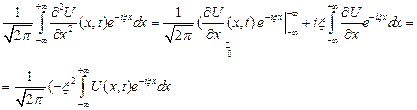
Следовательно, получаем, что преобразов. Фурье второй производной функции 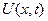связано с преобразованием Фурье самой функции 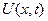следующ. равенством
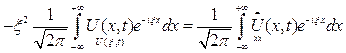
Применим преобразов. Фурье к исходному уравнению и нач. услов. сведя пост. задачу к задаче Коши для обыкновенного дифференциального уравнения
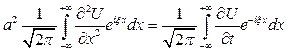
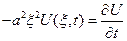
От первого уравнения осталось уравнение:
-
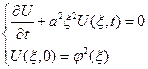Полученная задача, является задачей Коми для обыкновенного дифференц. уравнения.
Решением этой задачи является функция
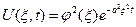(что проверяется простой подстановкой)
Покажем, что функция
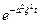является преобразованием Фурье
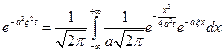
Т.е. явл. преобразов. Фурье от функции:
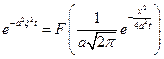
Док-во: считаем
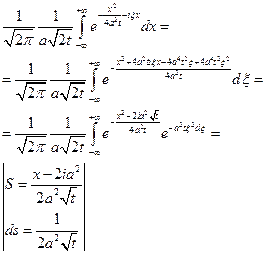
Мы доказали, что функция
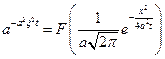
и наше решение
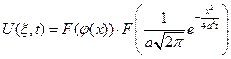
Решение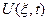 
можно записать в виде:
Как известно произведение двух преобразований Фурье = свертке преобраз. функций равна преобраз. Фурье от свертки преобразуемых функций
т.е.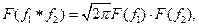 
где f1 свернутая с f2
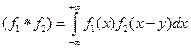
Тогда
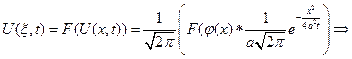
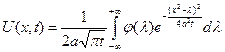
Получено решение исходной задачи Коши и назыв. формула Пуассона для решения задачи Коши уравнения теплопроводности.
Осталось проверить, что заданное уравнение удовлетворяет начальному условию, т.е.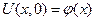 
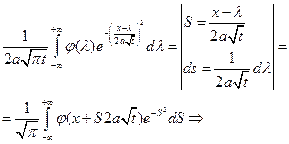
При 
находим, что
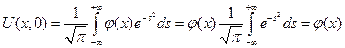ч.т.д.
Найденное решение удовлетворяет условию:
Пример:
,
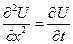
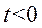
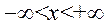
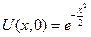
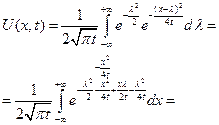
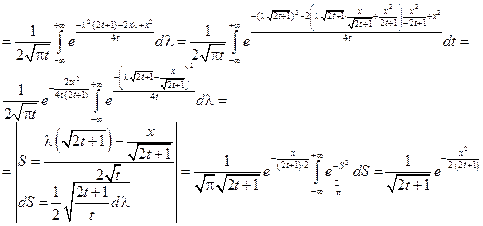Фундаментальное решение уравнения теплопроводности (
- функция Дирана)
Функция
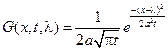
Входящая в формулу Пуассона назыв. фундаментал. решение уравнений теплопроводности.
Рассматривая как функция аргументов x,t она удовлетворяет уравнению теплопроводности
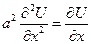в чем можно убедится проверкой.
Фундаментальное решение имеет важный физический смысл, связанный с понятием теплового импульса. Допустим в начальный момент времени начальное распределение температуры имеет вид:
 |
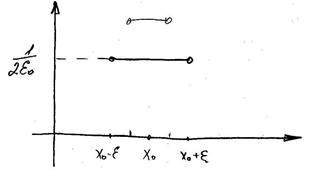Чем меньше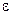 
тем выше полочка
Тогда в силу формулы Пуассона распределен. температуры в стержне имеет вид:
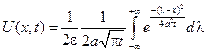
по теореме о среднем найдется такая точка
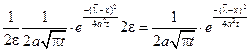, где 
устремим 
, тогда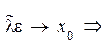 
из последнего равенства получим
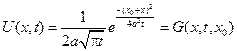- это означает, что функция 
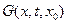представляет распределенную температуру в стержне в момент 
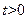, если начальный момент времени 
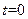в точке х0 имеется бесконечный пик температур, а в остальных точках стержня температура равна была 0. Такое начальное распределение температур может быть приближ. реализовано следующим образом:
В момент 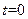к точке х0 стержня на очень короткий промежуток времени подносится узкое пламя очень высокой температуры (тепловой импульс) – это начальное распределение температур описыв. Формулой Дирана и обозначается 
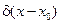. Не явл. функцией в обычном смысле 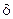функция определена формально при помощи соотношений
1. 
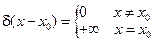
2. 
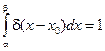для любого интервала 
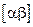, содерж. точку х0
3. 
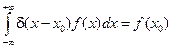
Таким образом фундамент. решение 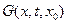явл. решением уравнения стержня при начальном распределение температур
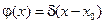
Д/з стр. 31
