.
Интегральными обычно называют уравнения, содержащие неизвестную функцию под знаком интеграла. Это определение не очень удачно. Под общим названием «интегральные уравнения» известны вещи, мало похожие одна на другую. Обычно не пытаются дать общего определения интегральным уравнениям, а ограничиваются тем, что перечисляют наиболее важные классы интегральных уравнений.
Одним из наиболее важных и хорошо исследованных классов линейных интегральных уравнений является уравнение Фредгольма II рода. Так называют уравнение вида:
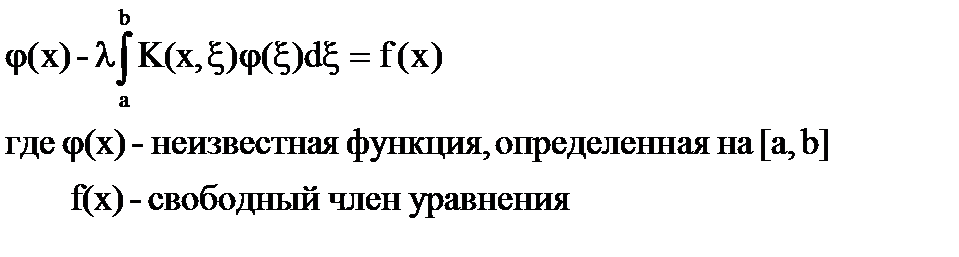 (1)
(1)
(в отличие от уравнений вида 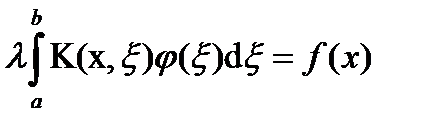 , которое называется уравнением I рода и не имеет большого практического значения).
, которое называется уравнением I рода и не имеет большого практического значения).
Если f(x)=0, то интегральное уравнение называется однородным; в противном случае – неоднородным.
Функцию двух действительных переменных 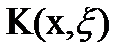 называют ядром уравнения; параметр λ – комплекснозначный. Ядро определено в квадрате: a≤x, ξ≤b.
называют ядром уравнения; параметр λ – комплекснозначный. Ядро определено в квадрате: a≤x, ξ≤b.
О ядре 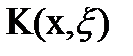 уравнения (1) предполагают, что
уравнения (1) предполагают, что
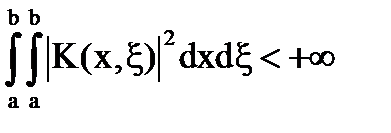 (2)
(2)
Свободный член f(x) уравнения (1) удовлетворяет неравенству
|
|
|
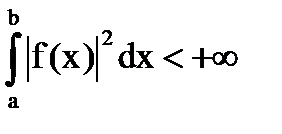 (3)
(3)
Аналогичное неравенство предполагается выполненным для неизвестной функции φ(x).
В случае (3) функцию f(x) называют суммируемой в (a, b). Ядро интегрального уравнения предполагается квадратично суммируемым в квадрате a≤x, ξ≤b.
Фредгольмом был изучен случай, когда φ(x), f(x) – непрерывны на [a, b], а
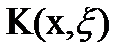 - непрерывно в основном квадрате a≤x, ξ≤b. Очевидно, в этом случае справедливо (3).
- непрерывно в основном квадрате a≤x, ξ≤b. Очевидно, в этом случае справедливо (3).
Например:

. Уравнение
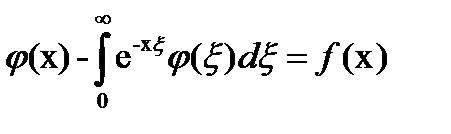 - не фредгольмово,
- не фредгольмово,
т.к. 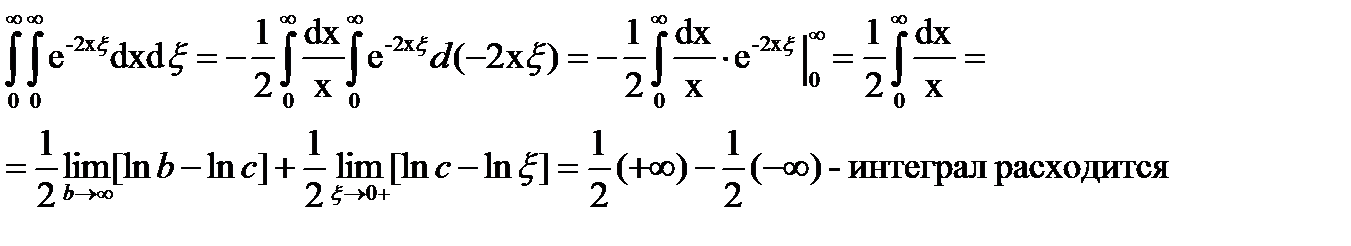

Интегральное уравнение вида (1) называется интегральным уравнением со слабой особенностью, если ядро уравнения
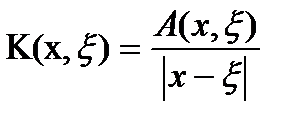 ,
,
где 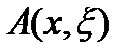 - непрерывная функция при a≤x, ξ≤b. В этом случае уравнение называют также особым или сингулярным.
- непрерывная функция при a≤x, ξ≤b. В этом случае уравнение называют также особым или сингулярным.
Вообще, интегральное уравнение называют особым, если либо а, либо b бесконечны; или ядро обращается в бесконечность в одной или нескольких точках рассматриваемого интервала.
Частным случаем уравнения (1) является уравнение вида:
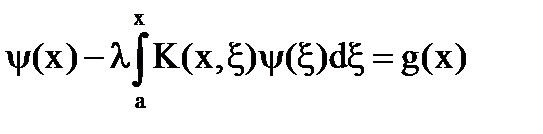 (4)
(4)
Это уравнение называется уравнением Вольтерра II рода.
Аналогично, уравнение
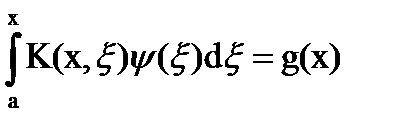
называется уравнением Вольтерра I рода (их мы рассматривать не будем).
Свойства интегрального уравнения, его решений определяется свойствами его ядра.
Для данного ядра 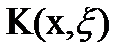 рассматриваются:
рассматриваются:
1) транспонированное ядро 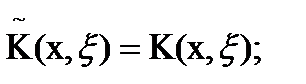 (5)
(5)
2) сопряженное ядро 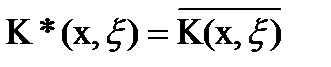 (6)
(6)
Если 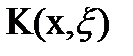 принимает лишь действительные значения, то
принимает лишь действительные значения, то 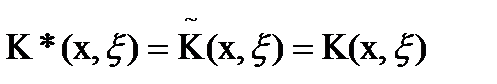 .
.
Данное ядро 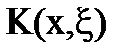 называют:
называют:
симметричным, если 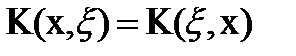 ,
,
эрмитовым, если имеет 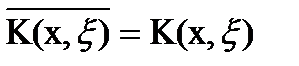 ,
,
нормируемым, если имеет место (2) и интеграл≠0,
непрерывным в среднем, если
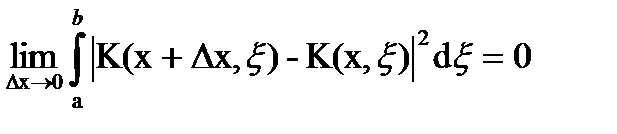 ,
,
вырожденным (или разделяющимся), если
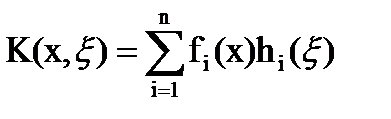 .
.
Линейным интегральным оператором называется преобразование (отображение)
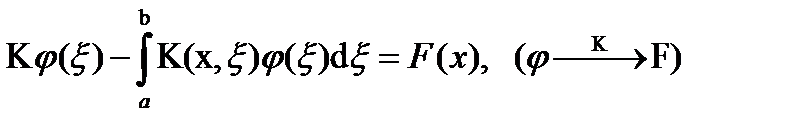
Уравнение (1) можно записать: 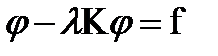 (7)
(7)
Интегральное уравнение Вольтерра II рода сводится к уравнению Фредгольма на (0, ∞), если ввести новое ядро
|
|
|
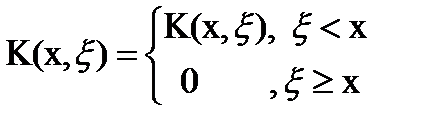
Решением интегрального уравнения называется функция φ(x), которая при подстановке в уравнение обращает его в тождество относительно 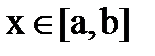 .
.
-------------------------------------------------------------------------------------------------
Пример. Проверить, является ли решением интегрального уравнения
Решение:
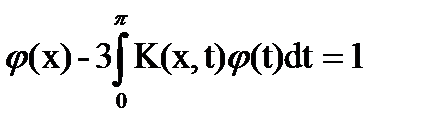 ,
,
где 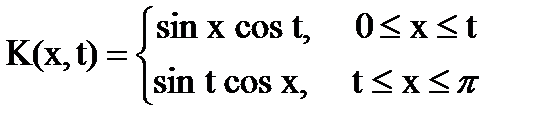 Функция
Функция 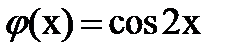
Решение:
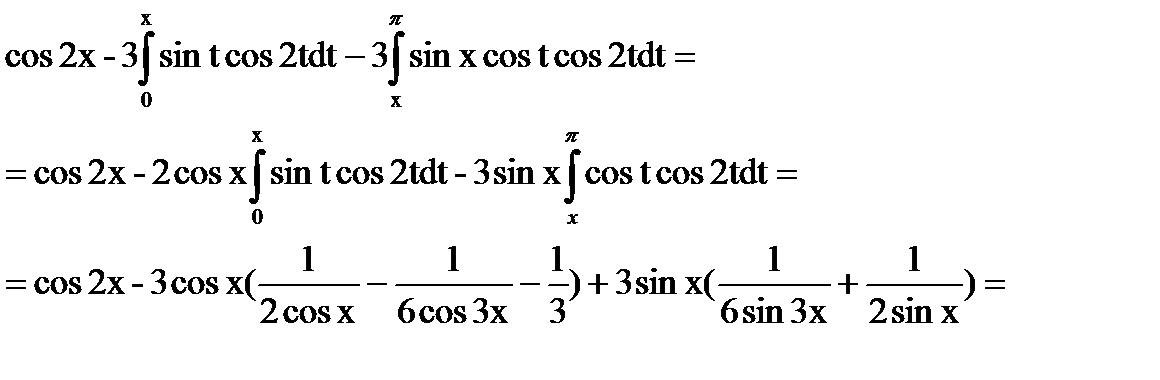
Интегрируем по частям:
а) 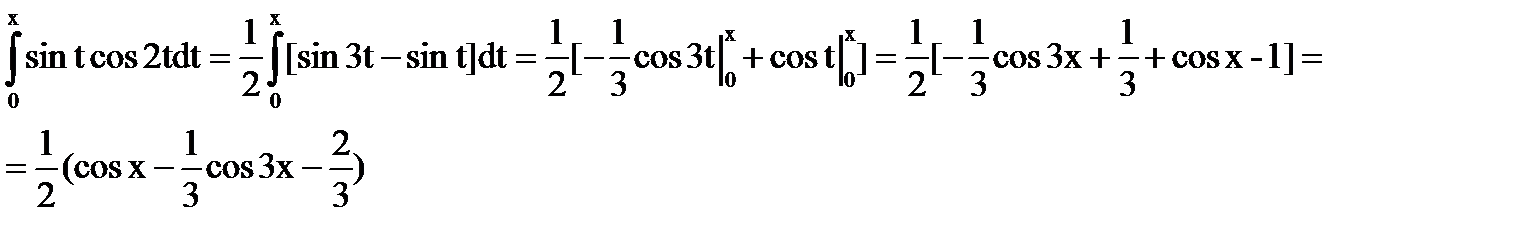
б) 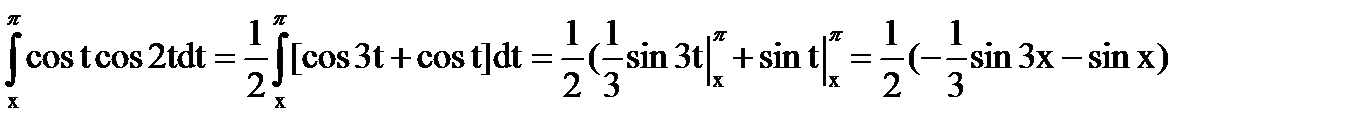
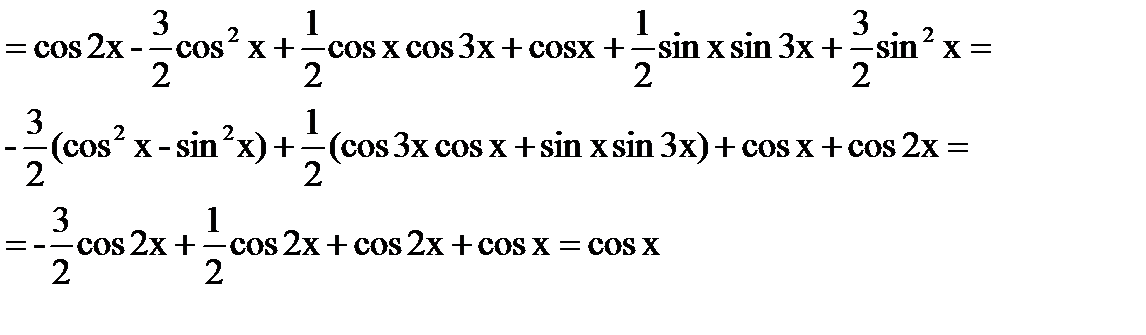
Ответ: Функция 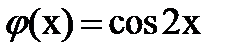 является решением интегрального уравнения.
является решением интегрального уравнения.
Задание для самостоятельной работы:
1.Показать,что данные функции являются решениями соответствующих интегральных уравнений.
1. 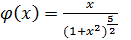 ;
; 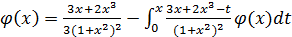
2. 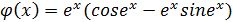
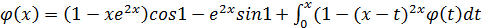
3. 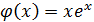 ;
; 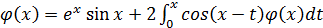
4. 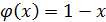 ;
; 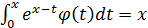
5. 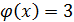 ;
; 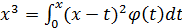
6. 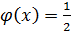 ;
; 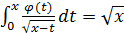
7. 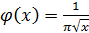 ;
; 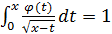
 2015-03-08
2015-03-08 3026
3026
