2015-03-08
1642
Рассмотрим уравнение
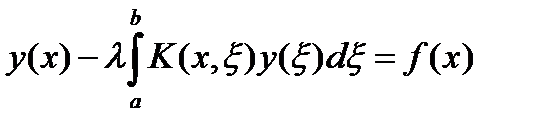(1)
где y(x), f(x) непрерывны на [a, b], а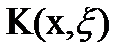 
- непрерывна в основном квадрате:
a≤x, ξ≤b.
Будем искать решение в виде ряда
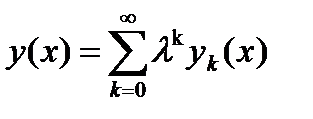, (9)
где функции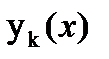 
подлежат определению.
Предположим, что ряд (9) равномерно сходится и y(x) – решение уравнения (1), тогда (9)→(1):
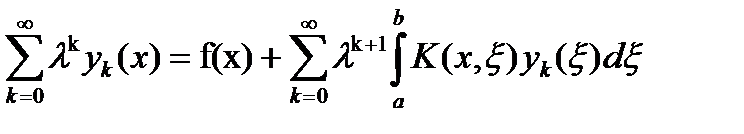
Приравняем коэффициенты в степенных рядах при одинаковых степенях λ, тогда
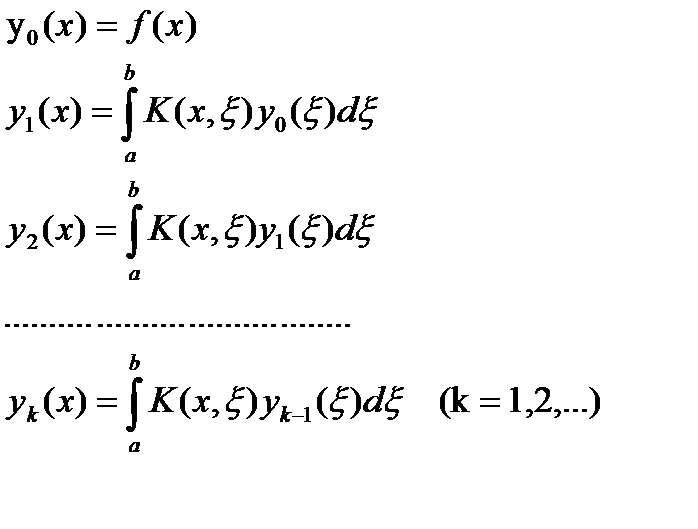(10)
Таким образом, формальное решение уравнения (1) определяется формулами (9)-(10).
Покажем, что ряд (9) действительно равномерно сходится (этим самым результат будет обоснован).
Так как 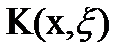и f(x) – непрерывны в замкнутых областях, то они ограничены:
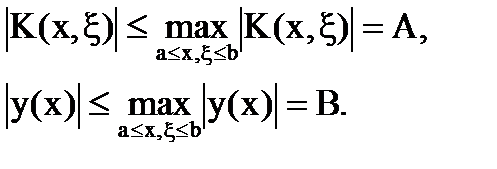Поэтому:
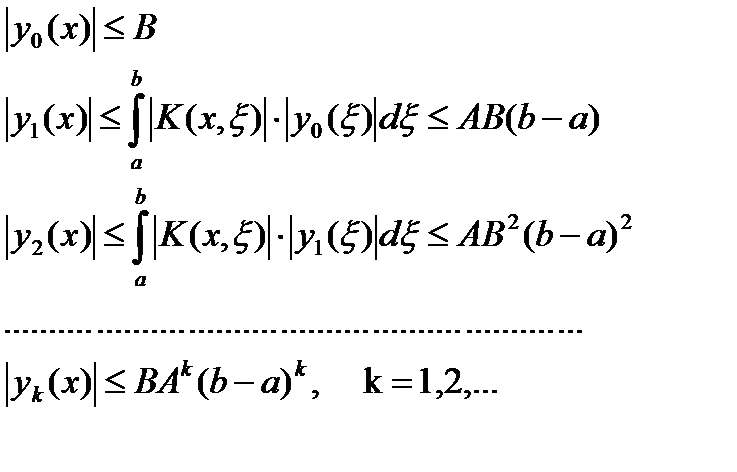
Значит ряд (9) мажорируется рядом
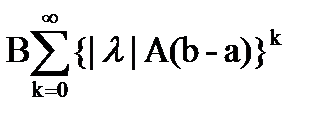- (11)
геометрический ряд – сходится, если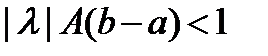 
, то есть при
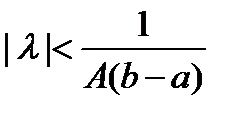(12)
Вывод: если имеет место (12), то ряд (9) сходится равномерно и абсолютно.
Замечания:
Решение линейного интегрального уравнения (1) было получено тремя различными методами и притом в трех различных формах. Приведенный метод – метод последовательных подстановок – был развит Нейманом, Лиувиллем и Вольтерра. Этот метод дает решение в виде степенного ряда относительно λ, причем коэффициенты при различных степенях λ являются функциями от х. Ряд сходится при λ, меньших по абсолютной величине, чем некоторое число (при малых λ). Этот метод называют еще «методом малого параметра».
|
|
|
Покажем теперь, что уравнение Фредгольма не может иметь более одного решения в классе ограниченных функций, если λ удовлетворяет неравенству (12).
Пусть y(x) и y*(x) – два ограниченных решения уравнения, тогда разность ω(x)=y(x)-y*(x) ограничена:
,
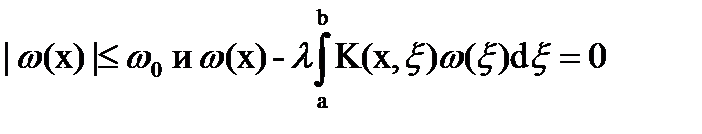то есть является решением однородного уравнения.
Имеем
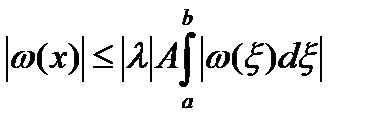, где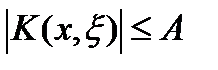 
при a≤x, ξ≤b.
Далее
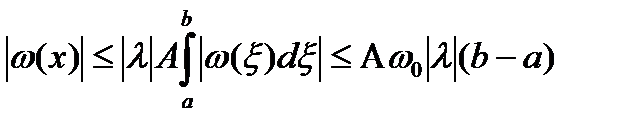
Заменяя в интеграле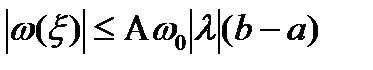 
, получим
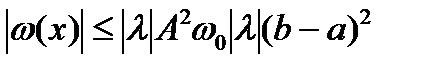и т.д.
После «k» шагов:
,
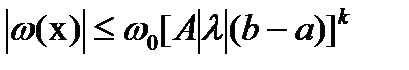но так как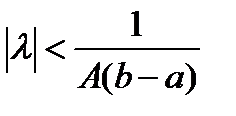 
, то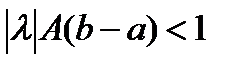 
и, следовательно, 
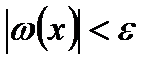, где ε>0 – любое число, => ω(x)=0 => y(x)=y*(x).
Замечание:
Значит, в круге 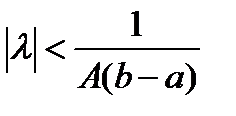нет собственных значений ядра.
