Было показано, что решение уравнения:
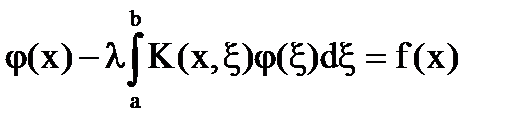 (1)
(1)
в том случае, если 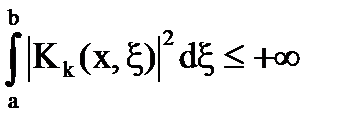 и
и 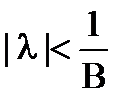 , где
, где 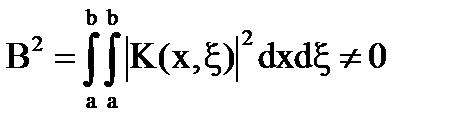
определяется по формуле:
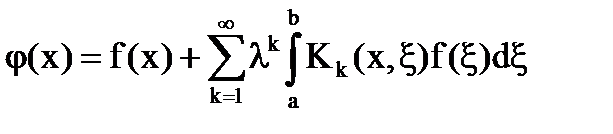 (19)
(19)
Так как ряд в (19) сходится равномерно, то можно изменить порядок суммирования и интегрирования:
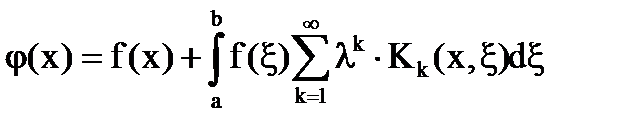
Обозначим 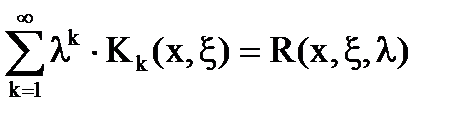 - ряд Неймана. (23)
- ряд Неймана. (23)
Эта функция называется резольвентой уравнения (1). Решение уравнения можно записать:
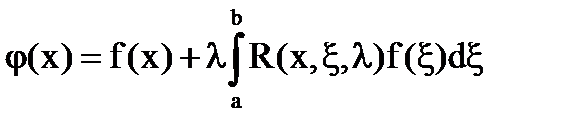 (24)
(24)
Если вычислена резольвента, то решение уравнения может быть записано сразу (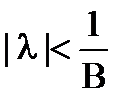 ).
).
Определение: Будем говорить, что интегральное уравнение (1) имеет резольвенту R(x,ξ,λ), если решение уравнения можно записать в виде (24), причем это решение единственное при любом свободном члене f(x).
Очевидно, что если у интегрального уравнения существует резольвента, то она единственная.
Действительно, пусть при 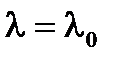 ,
, 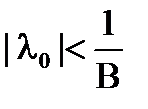 уравнение имеет две резольвенты
уравнение имеет две резольвенты 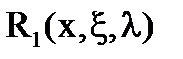 и
и 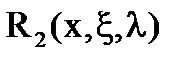 . Тогда единственное решение уравнения можно записать в виде:
. Тогда единственное решение уравнения можно записать в виде:
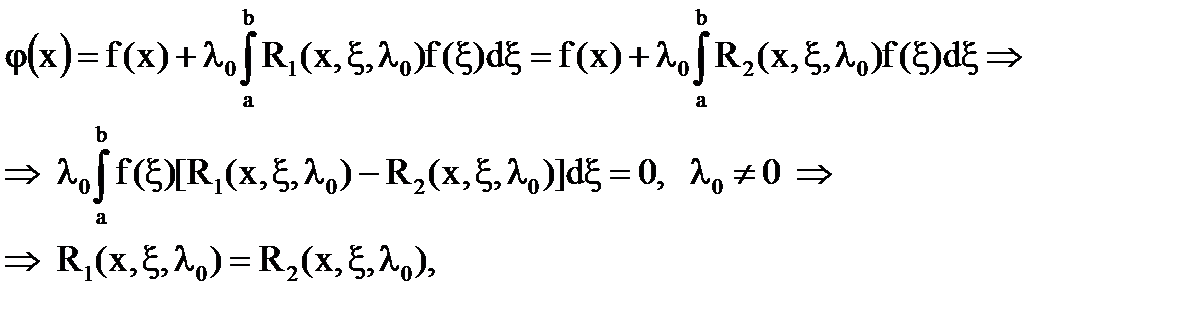
т.к. f(ξ) – произвольная функция.
Замечание: Резольвента была определена только для значений λ, таких что 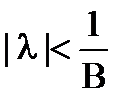 . Однако, резольвента существует во всей плоскости комплексного переменного λ, кроме некоторых изолированных значений λ.
. Однако, резольвента существует во всей плоскости комплексного переменного λ, кроме некоторых изолированных значений λ.
Пример.
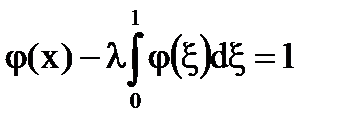 ,
, 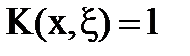 ;
; 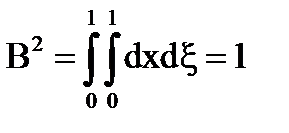
Ряд Неймана сходится при |λ|<1.
Обозначим
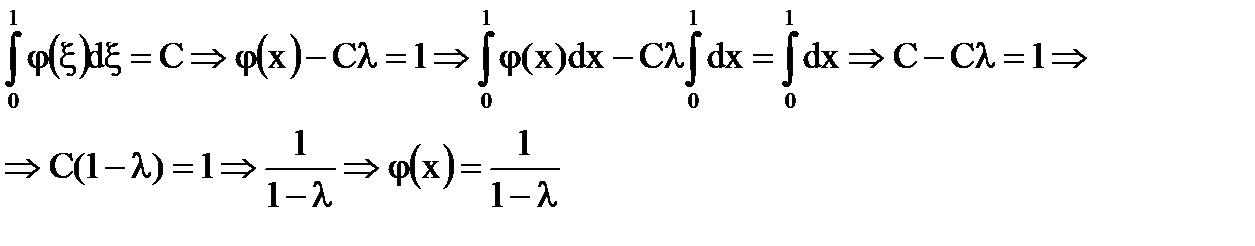
определенно при λ≠1 (внутри и вне окружности |λ|=1; на окружности, исключая лишь λ=1).
Замечание: Для некоторых уравнений Фредгольма ряд (23) сходится при всех λ.
Предположим, что 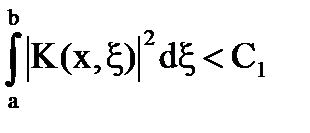 . Найдем оценку для итерированных ядер, пользуясь тем, что
. Найдем оценку для итерированных ядер, пользуясь тем, что 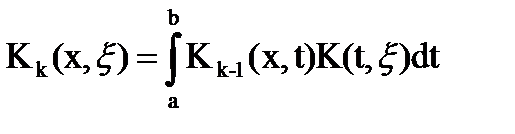
В силу неравенства Коши - Буняковского:
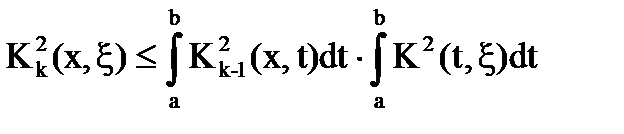
Проинтегрировав по ξ, получаем
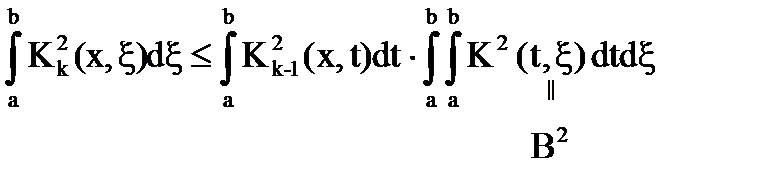
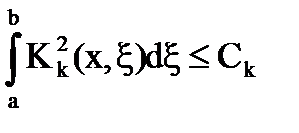
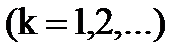
Имеем
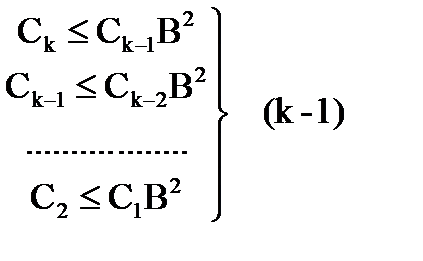 неравенств
неравенств
Отсюда 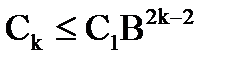 , то есть
, то есть 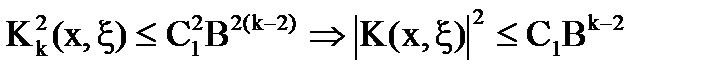
Значит, ряд 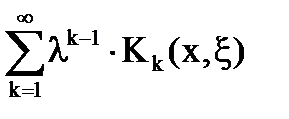 сходится при
сходится при 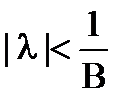 .
.
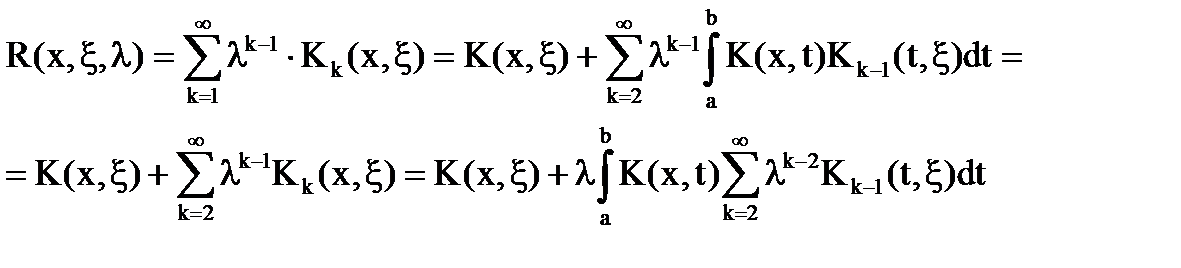
Отсюда резольвента удовлетворяет следующему интегральному уравнению:
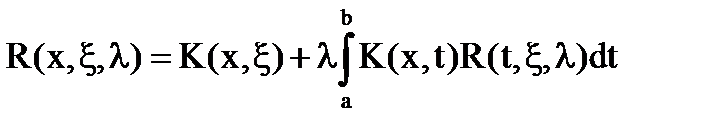 (25)
(25)
Допустим, что 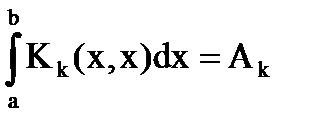
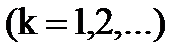
Этот интеграл называется «k»-тым следом ядра 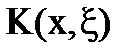 или следом «k»-го итерированного ядра. Имеем при x=ξ
или следом «k»-го итерированного ядра. Имеем при x=ξ
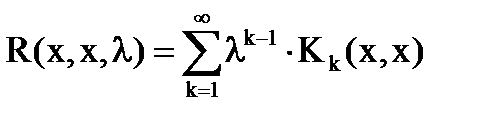
После интегрирования по x по [a,b]:
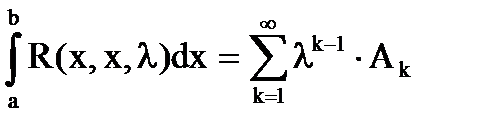 (26)
(26)
Пример. Построить резольвенту интегрального уравнения с помощью итерированных ядер.
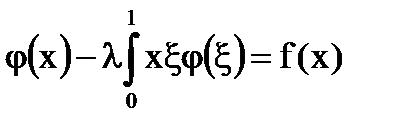
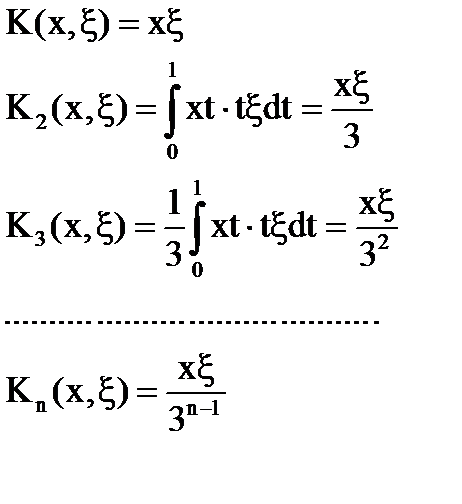
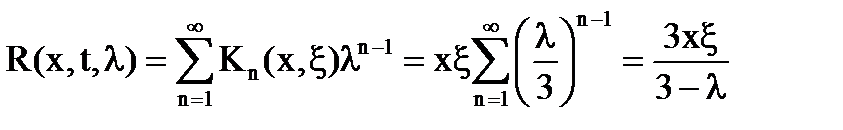 при |λ|<3
при |λ|<3
Решение интегрального уравнения:
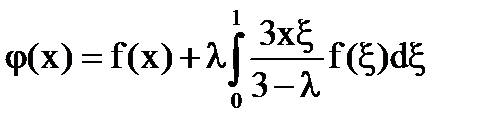
-----------------------------------------------------------------------------------------------
Задание для самостоятельной работы:
Найти итерированные ядра для указанных ядер при заданных a и b
и построить резольвенты.
Построение резольвенты для следующих ядер
1. 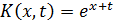 ; a=0, b=1
; a=0, b=1
2. 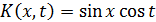 ; a=0,
; a=0, 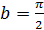
3. 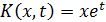 ; a=-1, b=1
; a=-1, b=1
4. 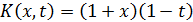 ; a=-1, b=0
; a=-1, b=0
5. 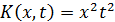 ; a=-1, b=1
; a=-1, b=1
6. 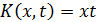 ; a=-1, b=1
; a=-1, b=1
Ответ 1) R(x,t,λ)= 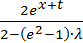 ;
; 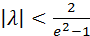
2) R(x,t,λ)= 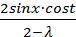 ;
; 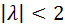
3) R(x,t,λ)= 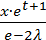 ;
; 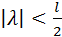
4) R(x,t,λ)= 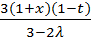 ;
; 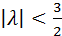
5) R(x,t,λ)= 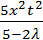 ;
; 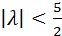
6) R(x,t,λ)= 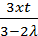 ;
; 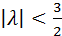
 2015-03-08
2015-03-08 4147
4147
