Существует важный класс интегральных уравнений, которые легко решаются путем сведения к системе алгебраических уравнений. Такими интегральными уравнениями являются с так называемыми вырожденными ядрами.
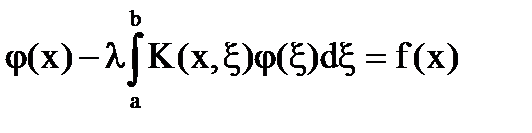 (1)
(1)
Определение: Ядро 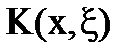 интегрального уравнения называется вырожденным, если его можно представить в виде суммы конечного числа слагаемых, каждое из которых есть произведение двух функций, причем первая зависит лишь от х, а вторая – только от ξ:
интегрального уравнения называется вырожденным, если его можно представить в виде суммы конечного числа слагаемых, каждое из которых есть произведение двух функций, причем первая зависит лишь от х, а вторая – только от ξ:
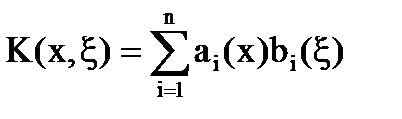 (27)
(27)
Считаем, что 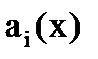 и
и 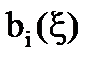 непрерывны на [a,b]
непрерывны на [a,b] 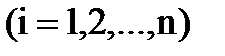 и что
и что 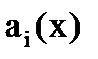 ,а также
,а также 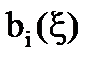 линейно независимы между собой.
линейно независимы между собой.
Уравнение (1) имеет вид:
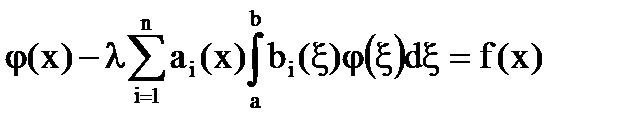
Обозначим 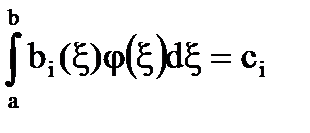
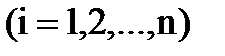 (28)
(28)
Тогда 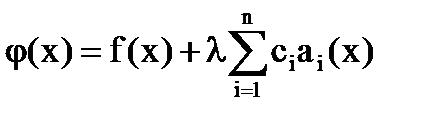 (29)
(29)
Подставим (29) в (1):
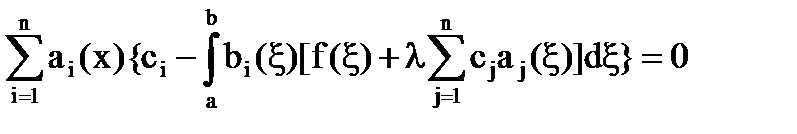
Так как 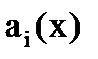
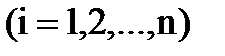 , линейно независимы, то
, линейно независимы, то
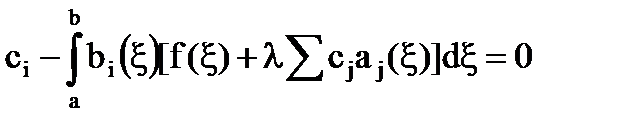
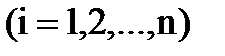
Обозначим: 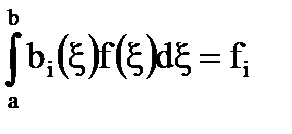 (30)
(30)
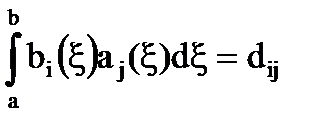 ,
, 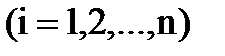 (31)
(31)
Тогда 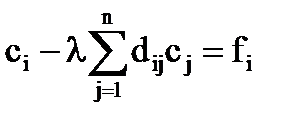
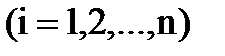 (32)
(32)
Решив систему (32), мы тем самым решим и данное интегральное уравнение, используя формулу (29). Если алгебраическая система (32) не разрешима, то таково и интегральное уравнение.
Определитель системы
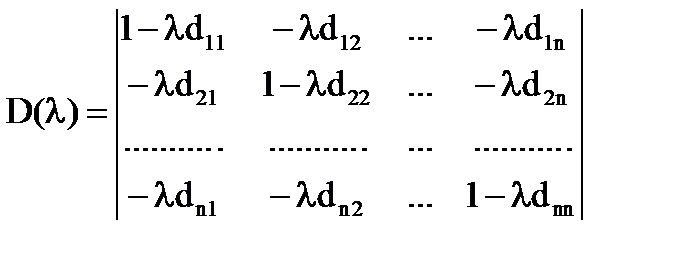 (33)
(33)
D(λ) – многочлен степени ≤ n, причем D(λ)≠0, так как при λ=0, D(0)=1. следовательно, D(λ) имеет ≤ n различных корней.
D(λ) называют определителем Фредгольма для уравнения (1).
1. Если λ таково, что D(λ)≠0, то система (32), а, следовательно, и уравнение (1) имеет единственное решение, определяемое формулой (29). В этом случае при f(x)=0, а следовательно, и 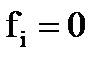
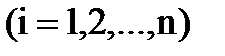 система (32) имеет единственное решение
система (32) имеет единственное решение 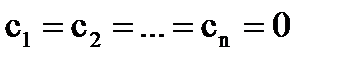 ; следовательно φ(х)=0. Это означает, что те λ, для которых D(λ)≠0, не является собственными значениями.
; следовательно φ(х)=0. Это означает, что те λ, для которых D(λ)≠0, не является собственными значениями.
Вывод: Если λ не является собственным значением, то уравнение (1) имеет единственное решение.
Очевидно, что для того, чтобы неоднородное уравнение (1) имело единственное решение при любой f(x) (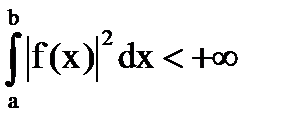 ), необходимо и достаточно, чтобы соответствующее ему однородное уравнение имело бы только тривиальное решение (φ(х)=0).
), необходимо и достаточно, чтобы соответствующее ему однородное уравнение имело бы только тривиальное решение (φ(х)=0).
Замечание: Как правило, при решении интегральных уравнений приходится часто прибегать к приближенным методам. При этом важно установить разрешимость уравнения при любой правой части (пользуясь первой теоремой). Удобнее бывает доказать, что однородное уравнение или транспонированное к нему (сопряженное) имеет лишь тривиальное решение. Отсюда в силу теоремы 1 следует разрешимость неоднородного уравнения.
Три фундаментальные теоремы Фредгольма, касающиеся разрешимости уравнений с вырожденными ядрами, можно распространить и на случай произвольного непрерывного ядра.
Формулы:
[1] 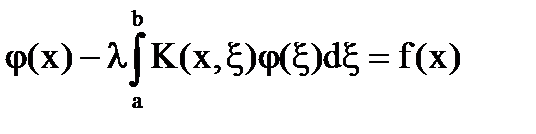
[2] 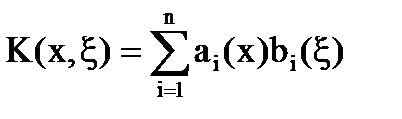
Решение уравнения:
[3]
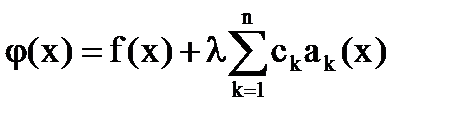
[5] 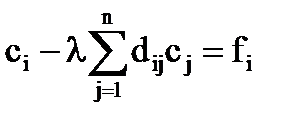 (i=1,2,…,n), где
(i=1,2,…,n), где
[6] 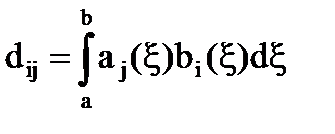
[7] 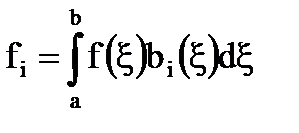
Примеры
Найти решение уравнений с вырожденными ядрами:
№1.
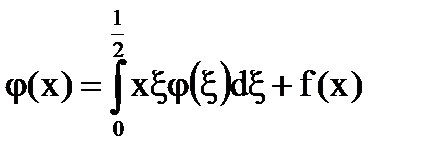
Решение: Обозначим 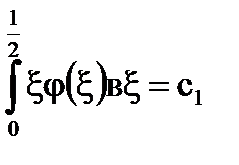 , получим
, получим 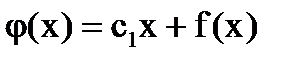 . Подставим в уравнение
. Подставим в уравнение 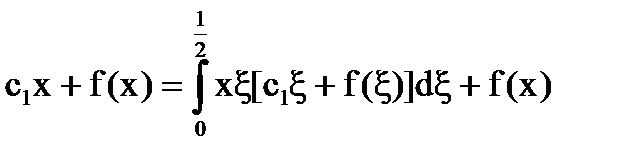
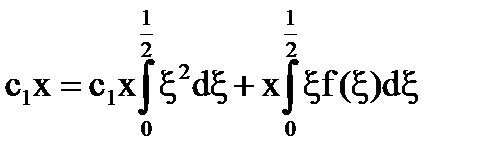 (
(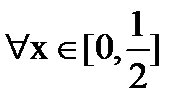 )
)
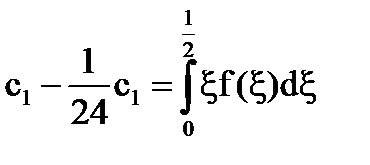 ;
; 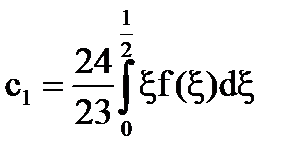
Ответ: 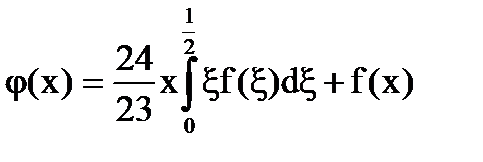
№2
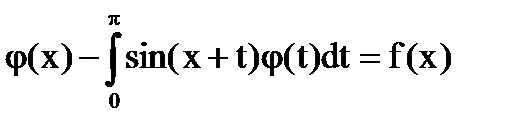
Решение: sin(x+t)=sinxcost+cosxsint
n=2; 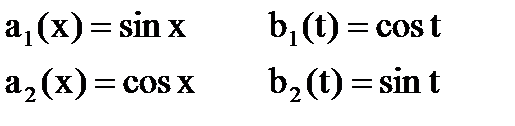
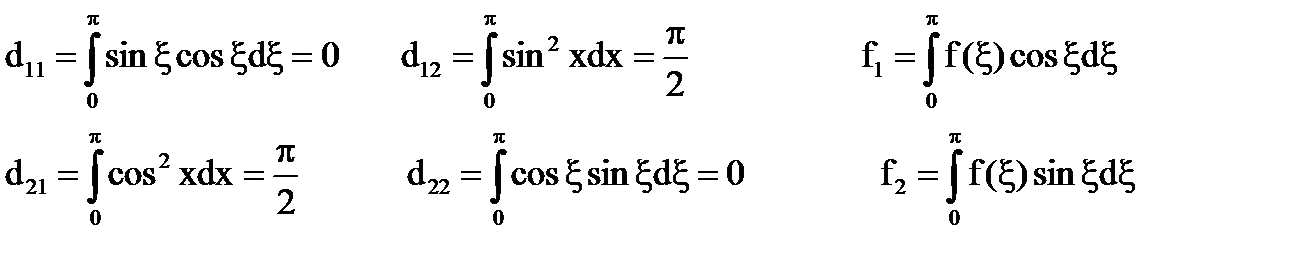
Система [5] имеет вид:
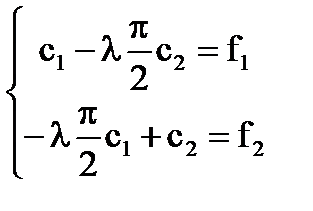
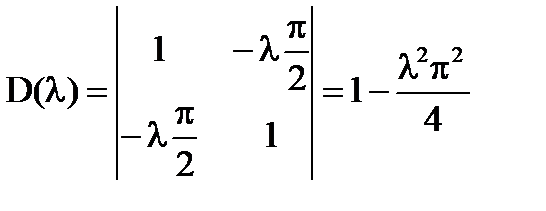
D(λ)=0; 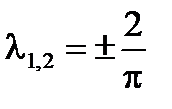 ;
; 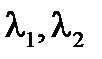 - собственные числа уравнения.
- собственные числа уравнения.
Если λ≠ 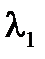 , λ≠
, λ≠ 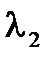 , то D(λ)≠0 и система имеет единственное решение:
, то D(λ)≠0 и система имеет единственное решение:
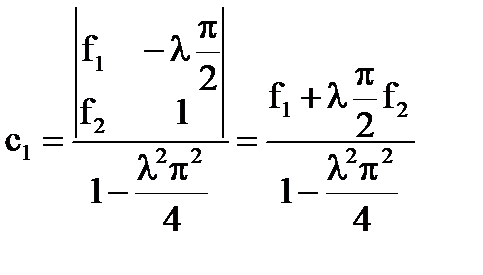
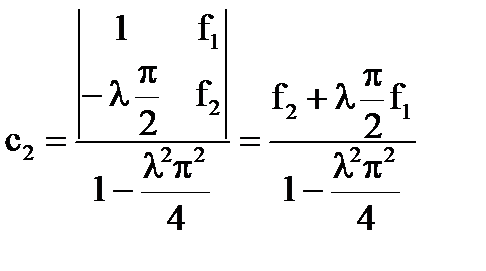
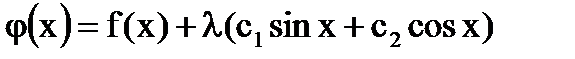
Ответ:
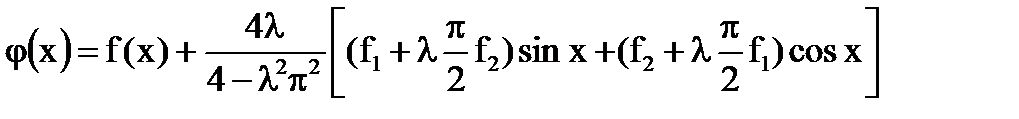 - единственное решение интегрального уравнения
- единственное решение интегрального уравнения
№3
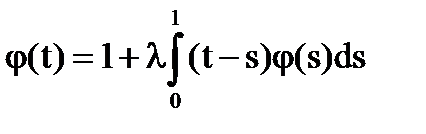
Решение:
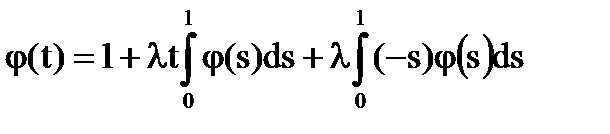
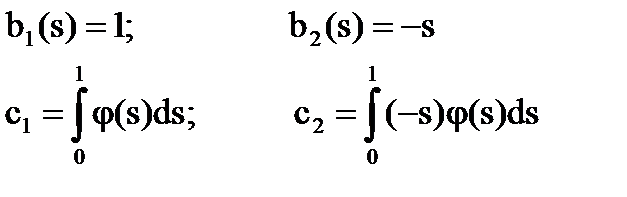
Тогда 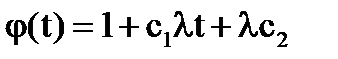
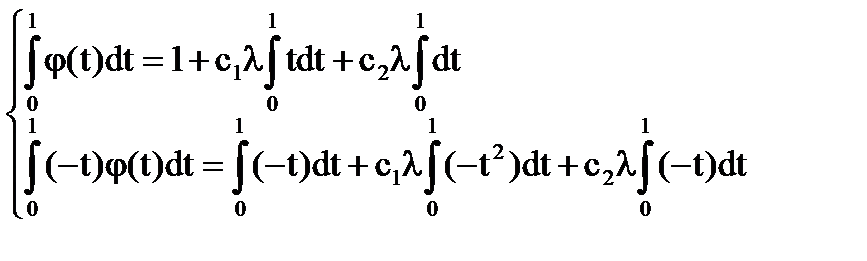
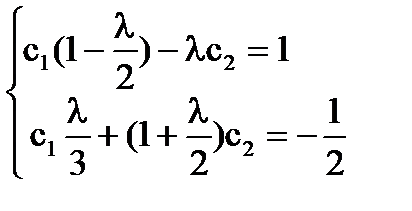
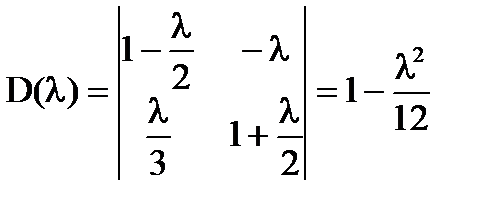
D(λ)≠0 при любых действительных λ.
По формулам Крамера 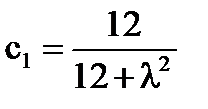 ;
; 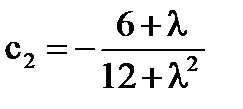
Если 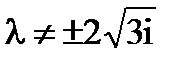 , то единственное решение уравнения
, то единственное решение уравнения
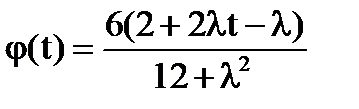
№4
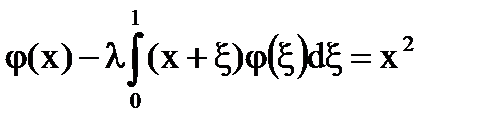
Решение: 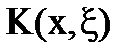 =x+ξ – непрерывно в квадрате 0≤х, ξ≤1 и является вырожденным.
=x+ξ – непрерывно в квадрате 0≤х, ξ≤1 и является вырожденным.
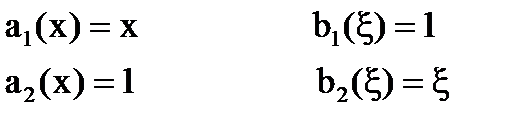
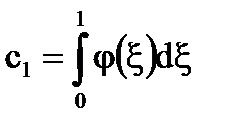 ;
; 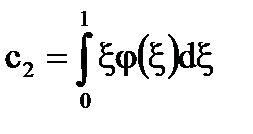
Тогда 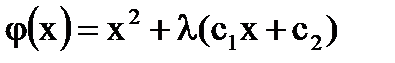
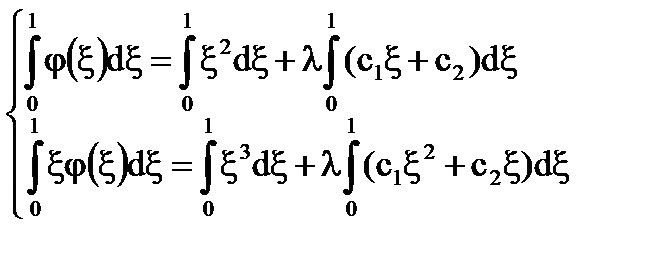
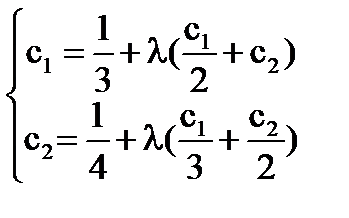 =>
=> 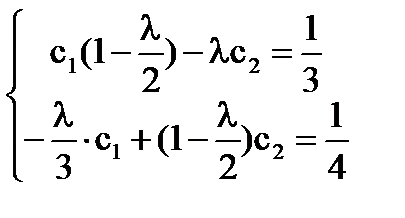
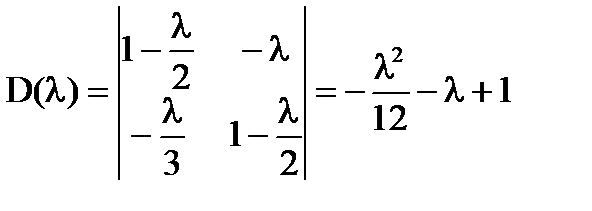
D(λ)=0 <=> 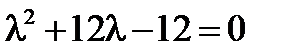 ,
, 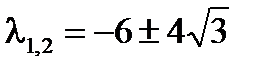
Если 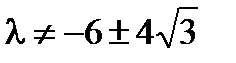 , то единственное решение
, то единственное решение
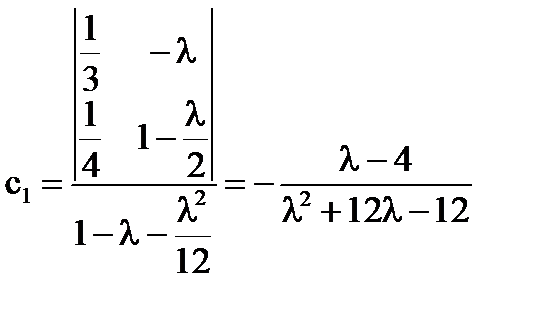
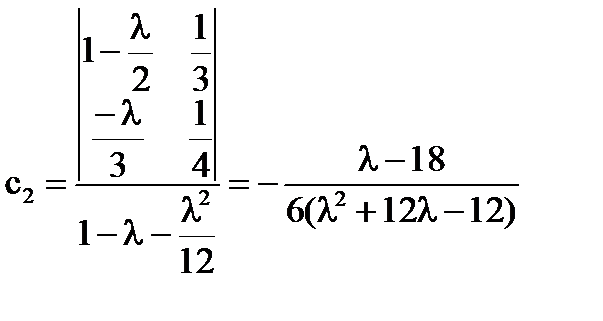
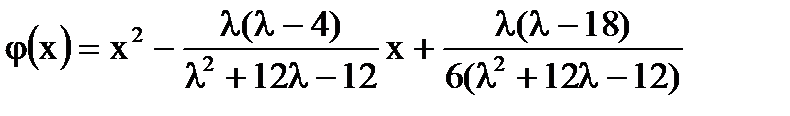 -
-
единственное решение уравнения при 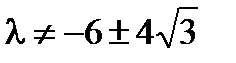 .
.
Замечание:
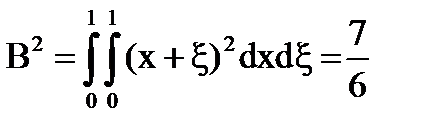
Решение существует, единственное и может быть найдено методом последовательных приближений при 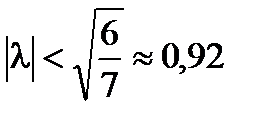 . При остальных λ последовательность приближений может расходиться, хотя решение существует (оно находится другим способом). Так как условия доказанной теоремы существования решения достаточные, но не являются необходимыми. Для уравнений с вырожденным ядром решение существует и единственно для всех λ, для которых D(λ)≠0.
. При остальных λ последовательность приближений может расходиться, хотя решение существует (оно находится другим способом). Так как условия доказанной теоремы существования решения достаточные, но не являются необходимыми. Для уравнений с вырожденным ядром решение существует и единственно для всех λ, для которых D(λ)≠0.
№5
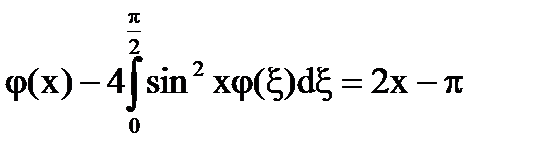
Решение:
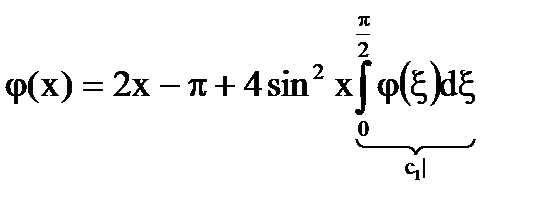
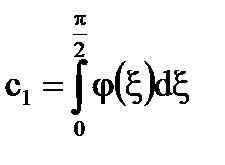 , тогда
, тогда 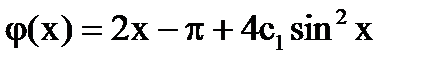 =>
=>
=> 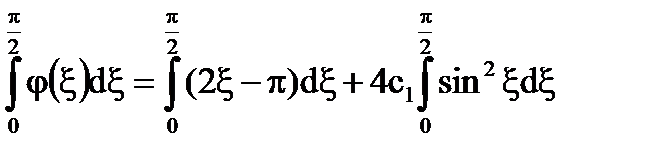
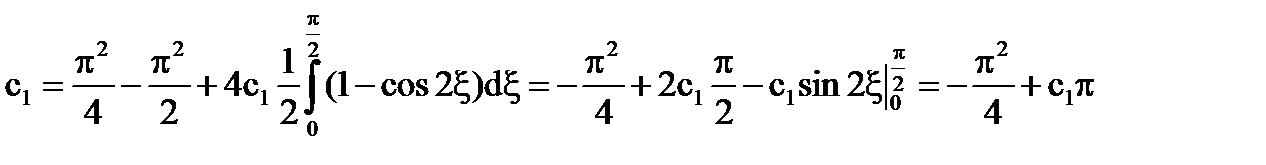
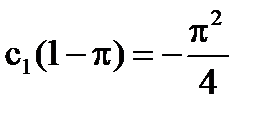 =>
=> 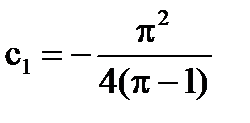
Ответ: 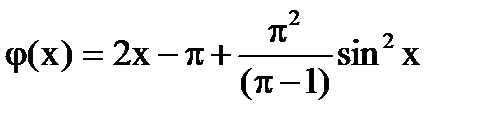
№6
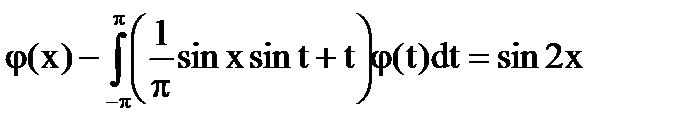
Решение: Ядро 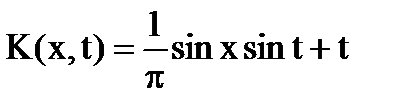 - вырожденное.
- вырожденное.
Полагая
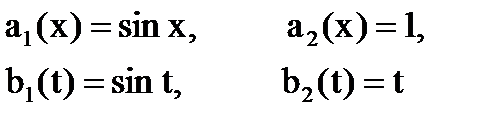
по формулам [6]-[7] вычисляем
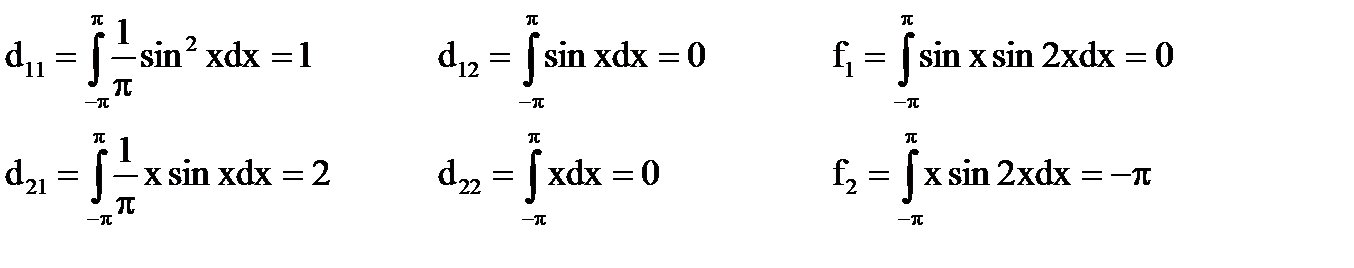
Система [5] принимает вид
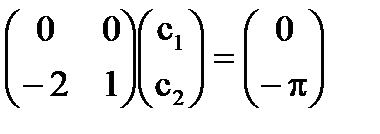 , ее общее решение:
, ее общее решение:
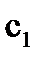 =С,
=С, 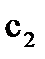 =-π+2С, где С – произвольна постоянная.
=-π+2С, где С – произвольна постоянная.
Ответ: Любая функция вида
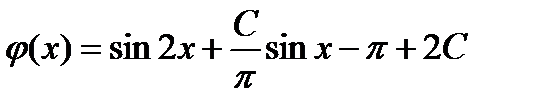
есть решение данного интегрального уравнения и других решений это уравнение не имеет.
Задание для самостоятельной работы:
Решить интегральные уравнения с вырожденными ядрами
1. 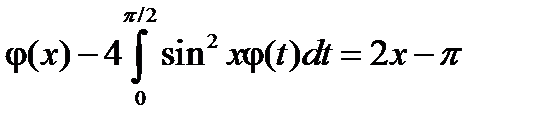
2. 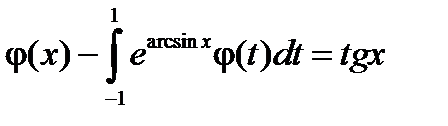
3. 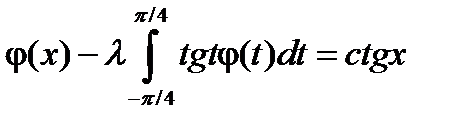
4. 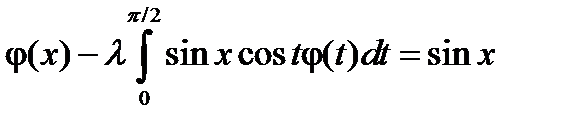
5. 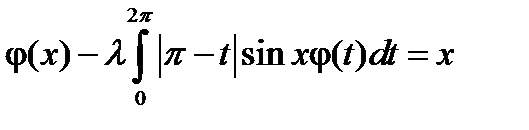
6. 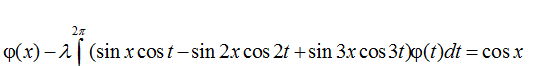
 2015-03-08
2015-03-08 5127
5127








