Общий вид этих уравнений таков:
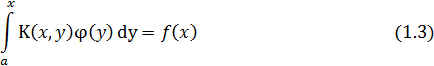
(уравнение Вольтерра первого рода) или
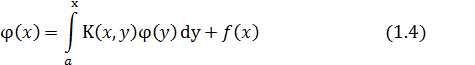
(уравнение Вольтерра второго рода). Ясно, что уравнение Вольтерра можно рассматривать как уравнение Фредгольма, в котором функция 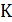 удовлетворяет условию
удовлетворяет условию
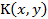 =0 при
=0 при 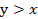 .
.
Однако уравнения вольтеровского типа целесообразно выделить в отдельный класс, поскольку они обладают рядом существенных свойств, не имеющих места для произвольных фредгольмовских уравнений.
Уравнения второго рода иногда записывают с параметром 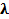
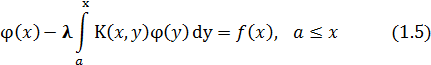
Тогда уравнение (1.5) представляет из себя не одно уравнение, а семейство уравнений, зависящее от параметра 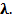
Если в уравнениях (1.1),(1.2),(1.3) или (1.4) функция 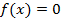 , то такое интегральное уравнение называется однородным. В противном случае уравнение называется неоднородным.
, то такое интегральное уравнение называется однородным. В противном случае уравнение называется неоднородным.
.
Пример 1. Показать, что функция 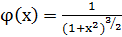 является решением интегрального уравнения Вольтерра
является решением интегрального уравнения Вольтерра
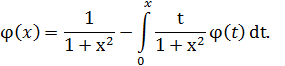
Решение. Подставляя вместо 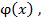 в правую часть уравнения функцию
в правую часть уравнения функцию 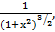 будем иметь
будем иметь
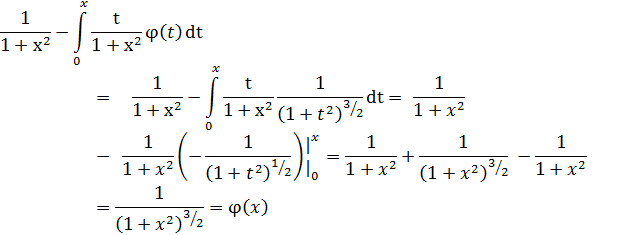
Таким образом,
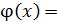
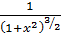 есть решение интегрального уравнения.
есть решение интегрального уравнения.
Пример 2. Показать, что функция 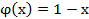 является решением интегрального уравнения Вольтерра
является решением интегрального уравнения Вольтерра
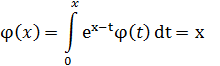
Решение. Подставляя вместо 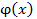 , в правую часть уравнения функцию
, в правую часть уравнения функцию 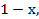 будем иметь
будем иметь
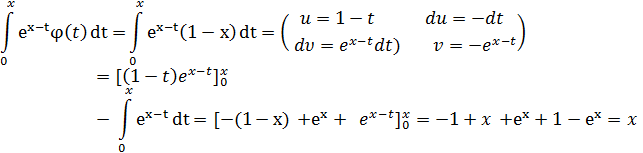
Таким образом, 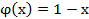 является решением интегрального уравнения Вольтерра.
является решением интегрального уравнения Вольтерра.
Пример 3. Показать, что функция 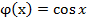 является решением интегрального уравнения Вольтерра
является решением интегрального уравнения Вольтерра
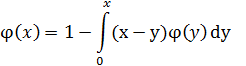
Получим
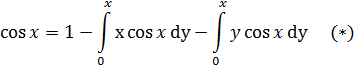
Находим первый интеграл
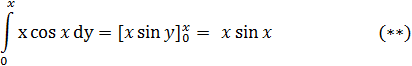
Находим второй интеграл
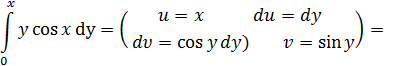
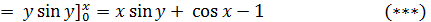
Подставим (***), (**) в (*)
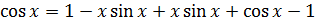
Таким образом, подстановка 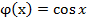 в обе части уравнения обращает его в тождество по х:
в обе части уравнения обращает его в тождество по х:
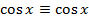
Это означает, согласно определению, что 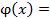
 есть решение интегрального ура
есть решение интегрального ура
внения.
.Можно заметить, если ядро 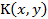 и
и 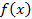 - непрерывно дифференцируемые функции, причем
- непрерывно дифференцируемые функции, причем 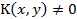 при
при 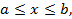 то интегральное уравнение Вольтерра I рода сводится к интегральному уравнению Вольтерра II рода.
то интегральное уравнение Вольтерра I рода сводится к интегральному уравнению Вольтерра II рода.
Дифференцируя уравнение Вольтерра I рода по х, имеем
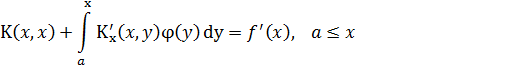
откуда получаем уравнение Вольтерра II рода
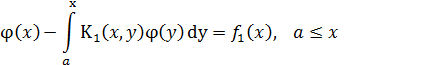
где 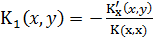 ,
, 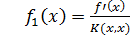
О ядре 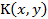 уравнения (1.5) предполагают, что
уравнения (1.5) предполагают, что
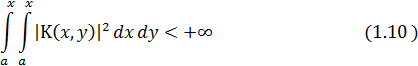
Свободный член f(x) уравнения (1.5) удовлетворяет неравенству

Аналогичное неравенство предполагается выполненным для неизвестной функции φ(x)

В случае (1.11) функцию f(x) называют суммируемой в (a, x), где x<b. Ядро интегрального уравнения предполагается квадратично суммируемым в квадрате a≤ x, y≤x.
Фредгольмом был изучен случай, когда φ(x), f(x) – непрерывны на [a,b], а 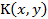 - непрерывно в основном квадрате a≤ x, y≤b. Очевидно, в этом случае справедливо (1.11).
- непрерывно в основном квадрате a≤ x, y≤b. Очевидно, в этом случае справедливо (1.11).
Интегральное уравнение Вольтерра II рода сводится к уравнению Фредгольма на (0, ∞), если ввести новое ядро
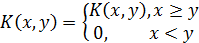 (1.16)
(1.16)
Уравнение Вольтерра II рода можно трактовать как уравнение Фредгольма II рода, ядро которого 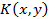 обращается в нуль при
обращается в нуль при 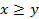 .
.
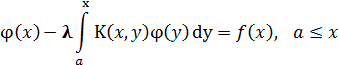
 2015-03-08
2015-03-08 4178
4178








