Решение уравнения Фредгольма 2-го рода:
Φ(x)-λ 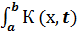 ф(t)dt=f(х) (1)
ф(t)dt=f(х) (1)
дается формулой
Φ(x)= f(х)+ λ 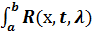 f(t)dt. (2)
f(t)dt. (2)
где функция R(х,t, λ), называемая резольвентой Фредгольма (1), определяется равенством
R(х,t, λ),= 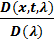 (3)
(3)
при условии, что D(λ)≠0. Здесь D(x,t,λ) и D(λ)-степенные ряды по λ
D(x,t,λ)=K(x,t) +∑ 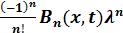 (4)
(4)
D(λ)=1+∑ 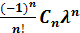 (5)
(5)
коэффициенты которых определяются
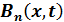 =
= 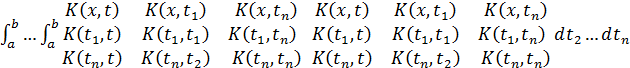
(6)
причем 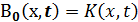
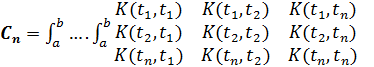 dt….d
dt….d 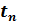 (7)
(7)
функция D(x,t,λ) называется минором Фредгольма, а D(λ) – определителем Фредгольма.
В случае, когда ядро K(x,t) ограничено или же интеграл
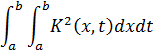
имеет конечное значение, ряды (4), (5) сходятся для всех значений λ и значит, является целыми аналитическими функциями от λ.
Пример. С помощью определителей Фредгольма найти резольвенту ядра K(x, t)=xet ; а=0, б=1.
Решение. Имеем В0 (x, t)= xet . Далее
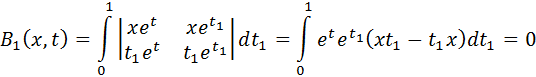
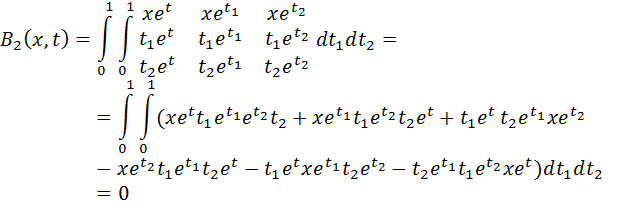
Так как определители под знаком интеграла равны нулю. Очевидно, что все последующие Вn(x,t)=0. Находим коэффициенты Сn.
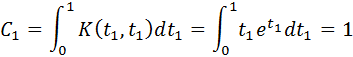
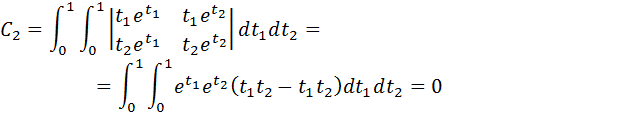
Очевидно, что все последующие Сn=0.
Согласно формулам (4) и (5) в нашем случае имеем:
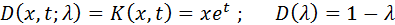
Таким образом, 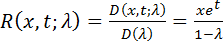
Применим полученный результат к решению интегрального уравнения
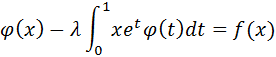
Согласно формуле (2)
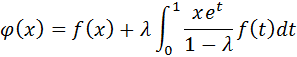
Пусть 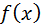 =e-x, то получим
=e-x, то получим
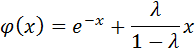
Задание для самостоятельной работы:
С помощью определителей Фредгольма найти резольвенту ядра K(x,t)
1) 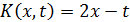
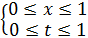
Ответ: 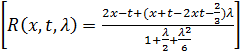
2) 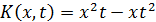
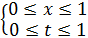
Ответ: 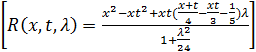
3) 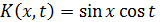
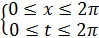
Ответ: 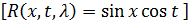
4) 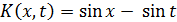
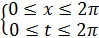
Ответ: 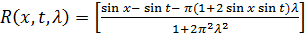
 2015-03-08
2015-03-08 3446
3446








