Решение. Обработку результатов наблюдений сведем к заполнению следующей таблицы

Обработку результатов наблюдений сведем к заполнению следующей таблицы. Комментарии по ее заполнению приведены ниже.

№ п/п	xi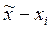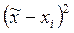
	16,20	-2,73	7,4256
	20,10	1,18	1,3806
	21,40	2,48	6,1256
	18,90	-0,03	0,0006
	16,50	-2,43	5,8806
	17,30	-1,63	2,6406
	18,20	-0,73	0,5256
	19,50	0,57	0,3306
	20,40	1,48	2,1756
	21,00	2,08	4,3056
	18,20	-0,73	0,5256
	19,40	0,47	0,2256
å	227,10	—	31,5425

1) Первые два столбца таблицы заполняем исходными данными.

2) В последнюю строке второго столбца записываем сумму всех чисел этого столбца .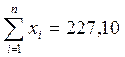

3) Вычисляем выборочное среднее по формуле: .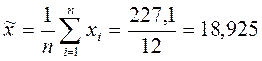

4) В каждую строку третьего столбца таблицы заносим величину 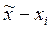, т.е. разность между выборочным средним 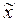и значением 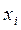, стоящим в этой же строке.

5) В каждую строку четвертого столбца заносим квадрат числа, стоящего в этой же строке в третьем столбце, и в последней строке вычисляем сумму чисел этого столбца: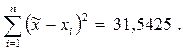

6) Вычисляем выборочную дисперсию по формуле: .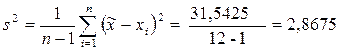

7) Вычисляем выборочное среднеквадратичное отклонение: .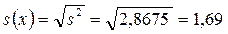

8) Вычисляем коэффициент вариации .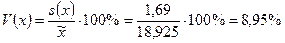

Коэффициент вариации показывает среднюю относительную величину разброса значений случайной величины X вокруг среднего значения в пределах выборки.

9) Доверительным называют интервал, в который с заданной наперед вероятностью g попадает среднее значение случайной величины для генеральной совокупности. В данной задаче под генеральной совокупностью понимается вся партия картофеля. Величина g называется доверительной вероятностью или уровнем надежности.

Доверительный интервал имеет вид: .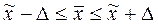

Величина 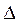представляет собой предельную ошибку выборки и для малых выборок (n£30) рассчитывается по формуле .

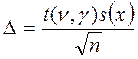Здесь:

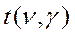— коэффициент Стьюдента. Таблицы для определения этой величины приведены в Приложениях;

n=n-1 —число степеней свободы.

В нашем случае n=12-1=11, g=0,95 и по таблицам находим: .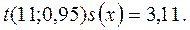

Отсюда 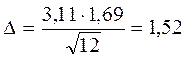и искомый доверительный интервал для генеральной средней имеет вид:

.

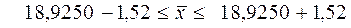
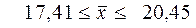Ответ: 1) 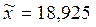. Это означает, что среднее содержание крахмала в исследованной партии из 12 клубней картофеля составляет 18,925%.

2) 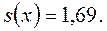Это среднее отклонение содержания крахмала в исследованной партии картофеля от выборочной средней .

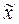3) Коэффициент вариации 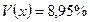. Он является мерой среднего относительного отклонения содержания крахмала в клубнях картофеля от выборочной средней в пределах пробной партии картофеля.

4) Доверительный интервал для генеральной средней на уровне надежности 0,95 представляет собой: 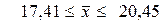. Иными словами, с вероятностью, равной 0,99, можно ожидать, что содержание крахмала во всей партии картофеля будет лежать в пределах от 17,41 до 20,45 процентов.