Глава 4. Градиент и производная по направлению

Пусть в каждой точке области D задана дифференцируемая функция двух переменных z = f (x, у). градиентом функции grad z в точке М(х, у) называется вектор, проекциями которого являются частные производные

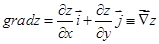. (4.1)

Аналогично определяется градиент функции трех переменных

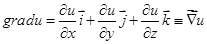(4.2)

Направление вектора градиента указывает направление наискорейшего изменения функции.

Длина вектор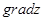а равна

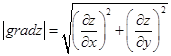(4.4)

Аналогично определяется и длина вектора .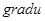

Для функции двух переменных в каждой точке М(х, у) вектор градиента перпендикулярен линии уровня.

Если задан вектор 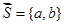. Производной функции по направлению вектора 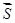называется проекция вектора градиента на направление вектора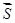

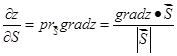. (4.5)

Т.е. проекция равна скалярному произведению векторов 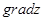и 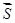делить на длину вектора .

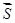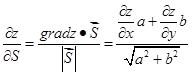(4.6)

Аналогично определяется производная по направлению вектора 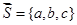и для функции трех переменных

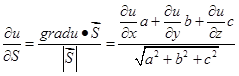(4.7)

Пример. Вычислить градиент функции 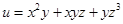в точке М(1,2,4) и производную по направлению .

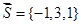Решение. Вычислим частные производные и найдем градиент функции

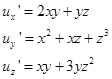
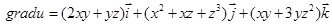(4.8)

Если в выражение (4.8) подставить координаты точки М, то получим градиент функции в точке М

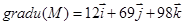
Вычислим производную по направлению вектора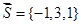

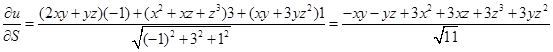
В точке М