3.1.2. Решить матричные уравнения:
а) 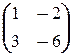 X =
X = 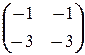 ; б) X
; б) X 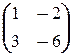 =
= 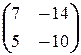 ;
;
в) 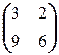 X =
X = 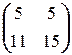 ; г) X
; г) X 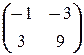 =
= 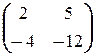 ;
;
д) 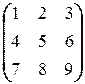 X =
X = 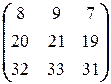 ; е) X
; е) X 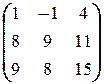 =
= 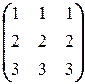 ;
;
ж) X 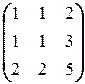 =
= 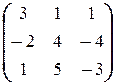 ; з)
; з) 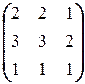 X =
X = 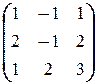 .
.
3.2.2. Найти все матрицы, перестановочные с данной матрицей (над полем R):
а) 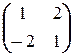 ; б)
; б) 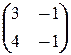 ; в)
; в) 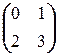 ; г)
; г) 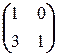 ;
;
д) 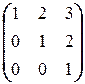 ; е)
; е) 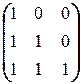 ; ж)
; ж) 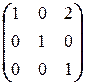 .
.
Приложения
Приложение 1. Варианты индивидуальных заданий.
Варианты индивидуальных заданий приведены ниже в таблице. Во всех вариантах предлагается выполнить следующие задания:
Задание 1. Решить системы методом Гаусса.
Задание 2. Решить систему используя:
а) матричный метод;
б) правило Крамера.
Задание 3. Исследовать систему на совместность и, в случае совместности, найти её решения в виде суммы частного и общего решения приведённой однородной.
Во всех заданиях сделать проверку.
| Вариант 1 | Вариант 2 | |
Задание 1 а) 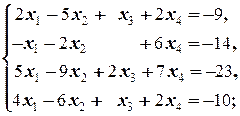 | Задание 1 а) 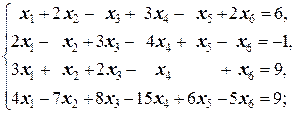 | |
б) 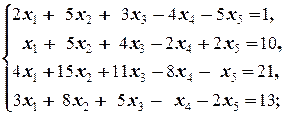 | б) 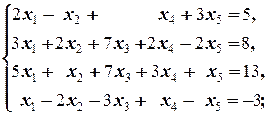 | |
в) 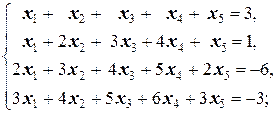 | в) 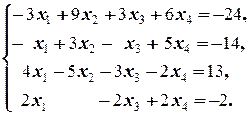 | |
Задание 2 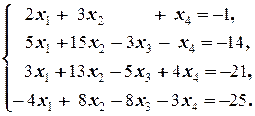 | Задание 2 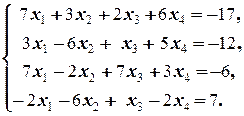 | |
Задание 3 а) 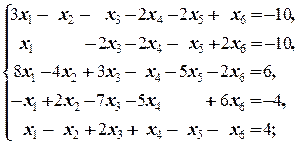 | Задание 3 а) 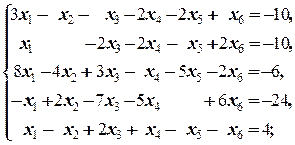 | |
б) 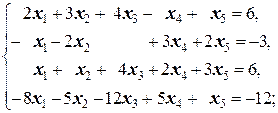 | б) 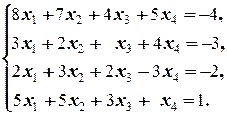 |
| Вариант 3 | Вариант 4 | |
Задание 1 а) 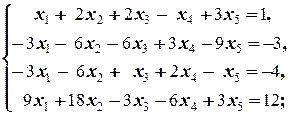 б) б) 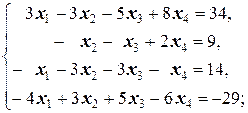 в) в) 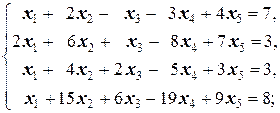 | Задание 1 а) 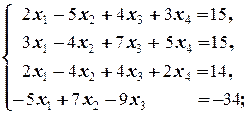 б) б) 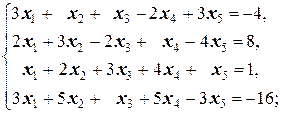 в) в) 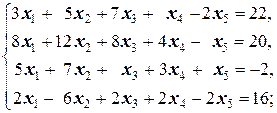 | |
Задание 2 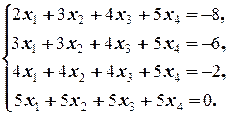 | Задание 2 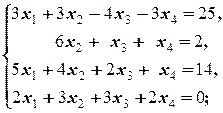 | |
Задание 3 а) 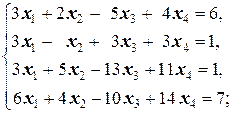 б) б) 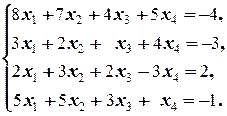 | Задание 3 а) 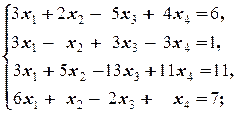 б) б) 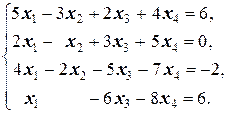 |
| Вариант 5 | Вариант 6 | |
Задание 1 а) 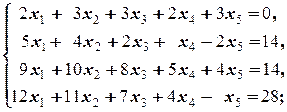 б) б) 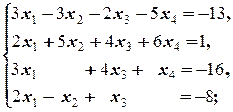 в) в) 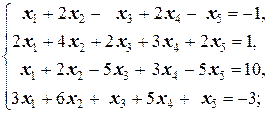 | Задание 1 а) 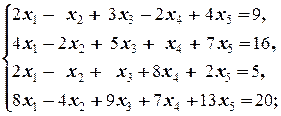 б) б) 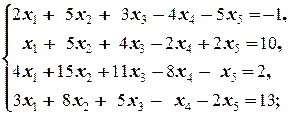 в) в) 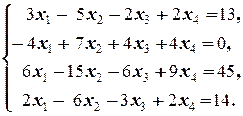 | |
Задание 2 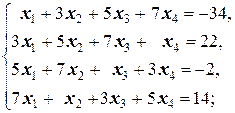 | Задание 2 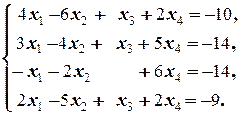 | |
Задание 3 а) 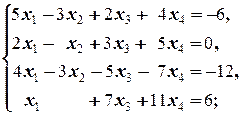 б) б) 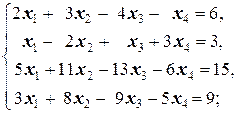 | Задание 3 а) 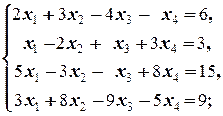 б) б) 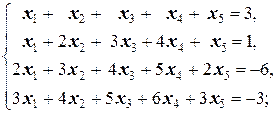 |
| Вариант 7 | Вариант 8 | |
Задание 1 а) 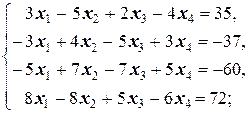 б) б) 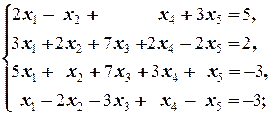 в) в) 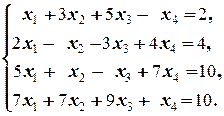 | Задание 1 а) 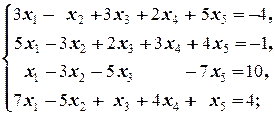 б) б) 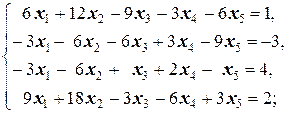 в) в) 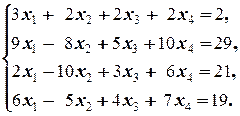 | |
Задание 2 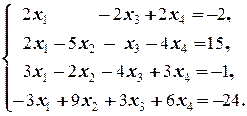 | Задание 2 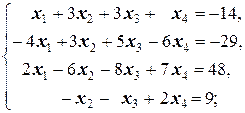 | |
Задание 3 а) 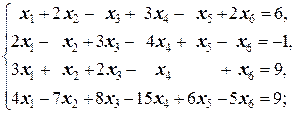 б) б) 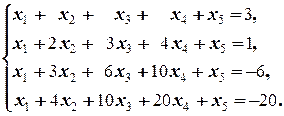 | Задание 3 а) 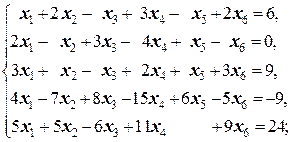 б) б) 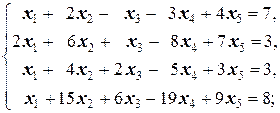 |
| Вариант 9 | Вариант 10 | |
Задание 1 а) 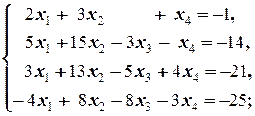 б) б) 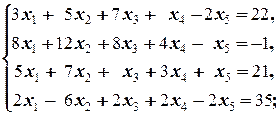 в) в) 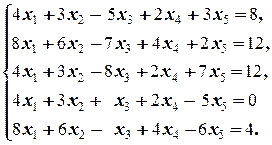 | Задание 1 а) 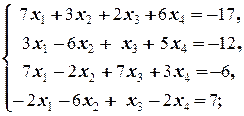 б) б) 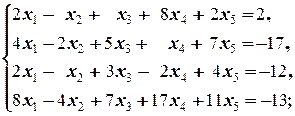 в) в) 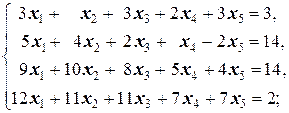 | |
Задание 2 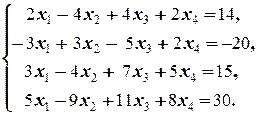 | Задание 2 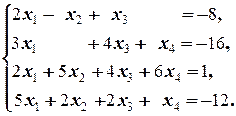 | |
Задание 3 а) 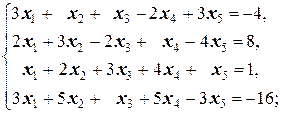 | Задание 3 а) 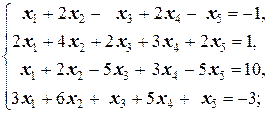 | |
б) 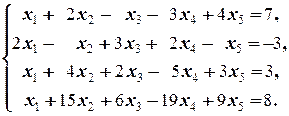 | б) 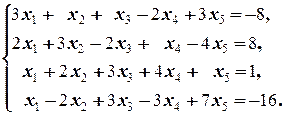 |
| Вариант 11 | Вариант 12 | |
Задание 1 а) 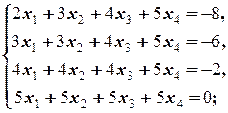 | Задание 1 а) 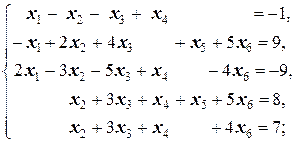 | |
б) 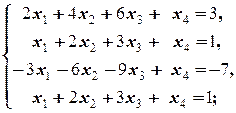 | б) 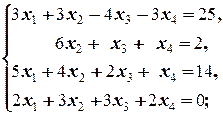 | |
в) 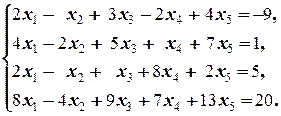 | в) 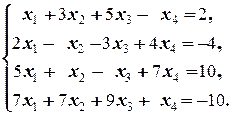 | |
Задание 2 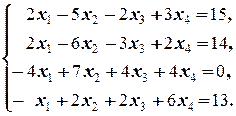 | Задание 2 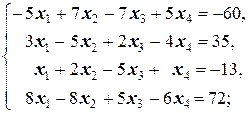 | |
Задание 3 а) 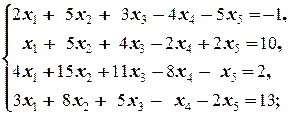 б) б) 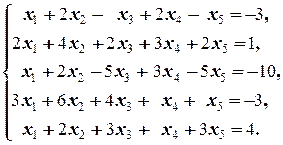 | Задание 3 а) 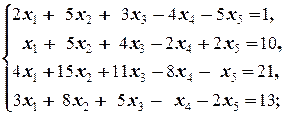 б) б) 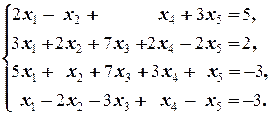 |
| Вариант 13 | Вариант 14 | |
Задание 1 а) 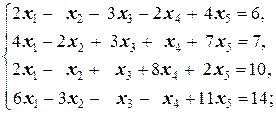 б) б) 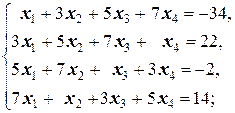 в) в) 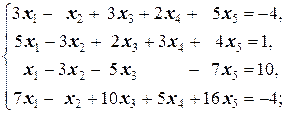 | Задание 1 а) 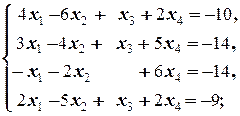 б) б) 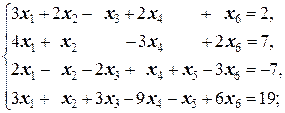 в) в) 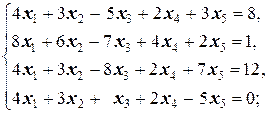 | |
Задание 2 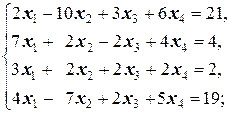 | Задание 2 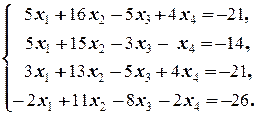 | |
Задание 3 а) 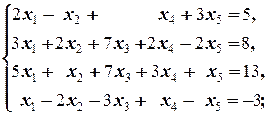 б) б) 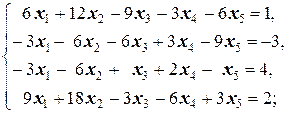 | Задание 3 а) 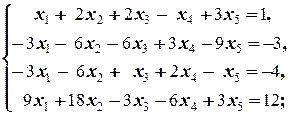 б) б) 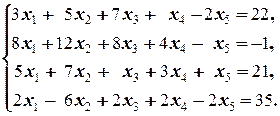 |
| Вариант 15 | Вариант 16 | |
Задание 1 а) 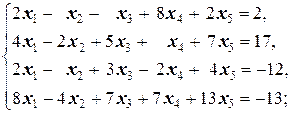 | Задание 1 а) 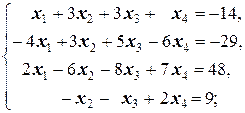 | |
б) 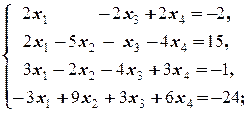 | б) 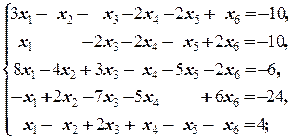 | |
в) 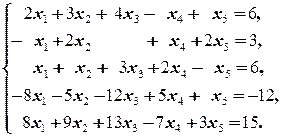 | в) 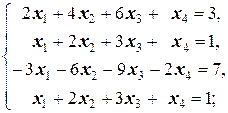 | |
Задание 2 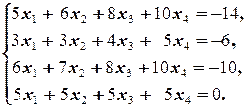 | Задание 2 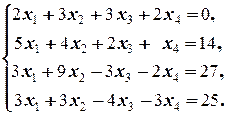 | |
Задание 3 а) 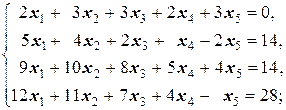 б) б) 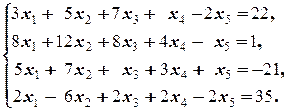 | Задание 3 а) 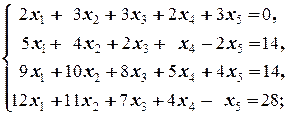 б) б) 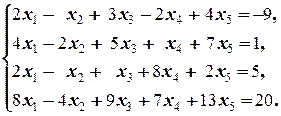 |
| Вариант 17 | Вариант 18 | |
Задание 1 а) 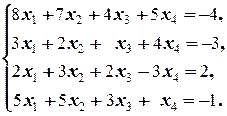 б) б) 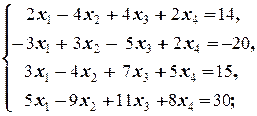 в) в) 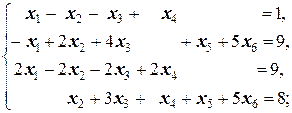 | Задание 1 а) 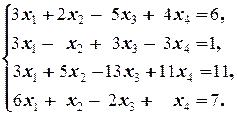 б) б) 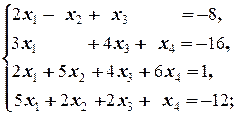 в) в) 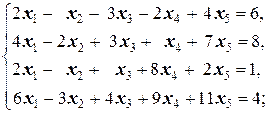 | |
Задание 2 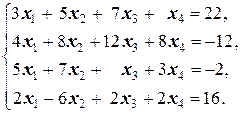 | Задание 2 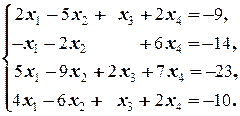 | |
Задание 3 а) 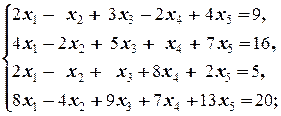 б) б) 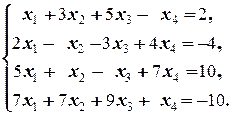 | Задание 3 а) 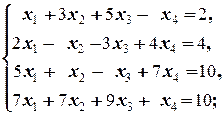 б) б) 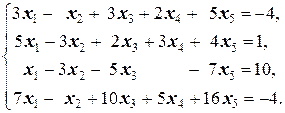 |
| Вариант 19 | Вариант 20 | |
Задание 1 а) 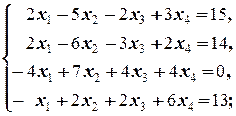 б) б) 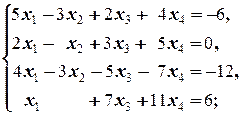 в) в) 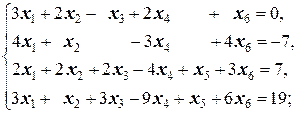 | Задание 1 а) 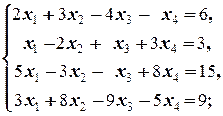 б) б) 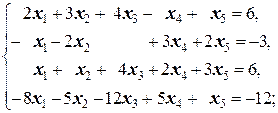 в) в) 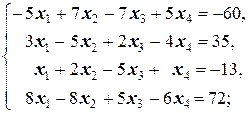 | |
Задание 2 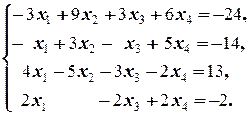 | Задание 2 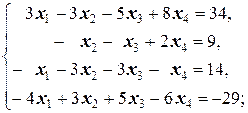 | |
Задание 3 а) 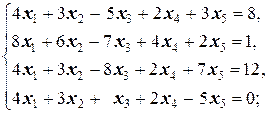 б) б) 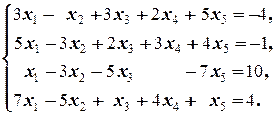 | Задание 3 а) 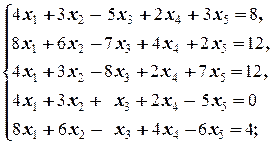 б) б) 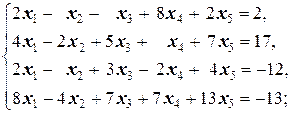 |
| Вариант 21 | Вариант 22 | |
Задание 1 а) 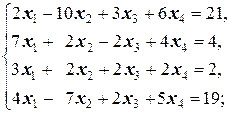 | Задание 1 а) 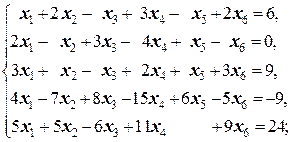 | |
б) 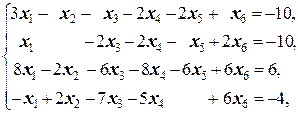 | б) 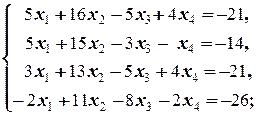 | |
в) 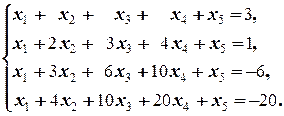 | в) 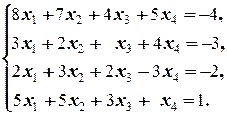 | |
Задание 2 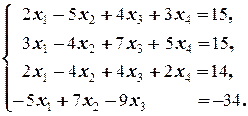 | Задание 2 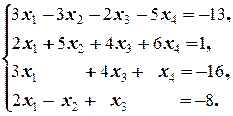 | |
Задание 3 а) 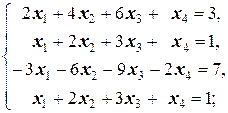 б) б) 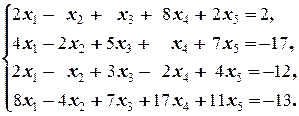 | Задание 3 а) 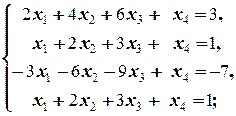 б) б) 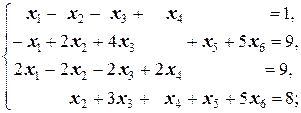 |
| Вариант 23 | Вариант 24 | |
Задание 1 а) 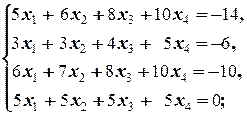 б) б) 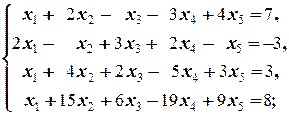 в) в) 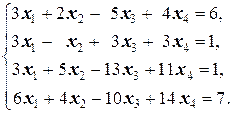 | Задание 1 а) 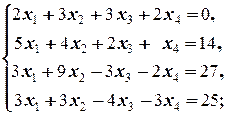 б) б) 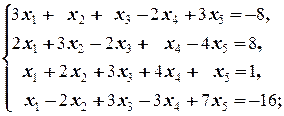 в) в) 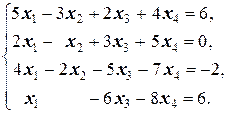 | |
Задание 2 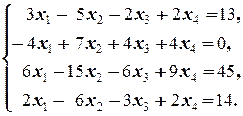 | Задание 2 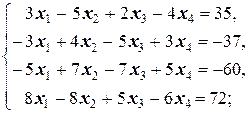 | |
Задание 3 а) 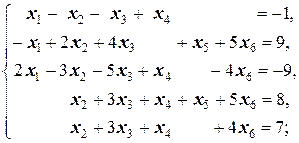 | Задание 3 а) 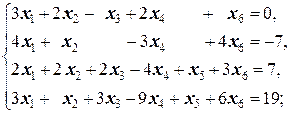 | |
б) 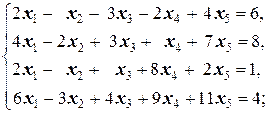 | б) 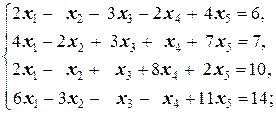 |
| Вариант 25 | Вариант 26 | |
Задание 1 а) 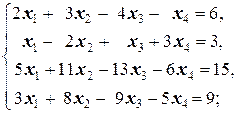 | Задание 1 а) 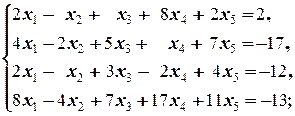 | |
б) 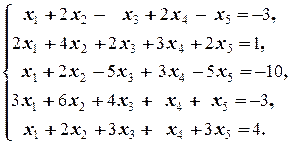 | б) 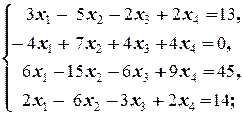 | |
в) 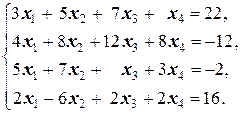 | в) 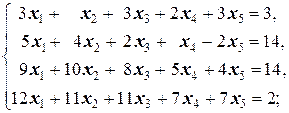 | |
Задание 2 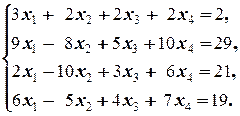 | Задание 2 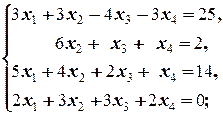 | |
Задание 3 а) 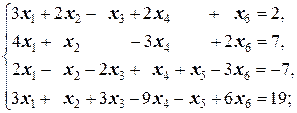 | Задание 3 а) 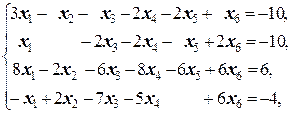 | |
б) 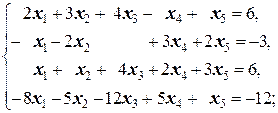 | б) 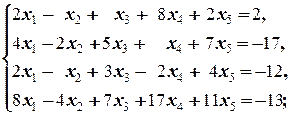 |
Приложение 2. Образец выполнения индивидуального задания.
1. Решить системы методом Гаусса:
a) 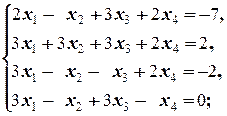 б)
б) 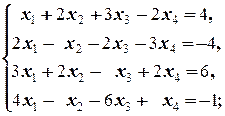
в) 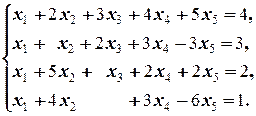
Неопределённую систему решить также методом Жордана-Гаусса
Решение. Метод Гаусса заключается в том, что с помощью последовательного применения элементарных преобразований из 2-го и остальных уравнений исключается неизвестная x 1, из 3-го и остальных уравнений исключается неизвестная x 2 и т.д., и так до тех пор, пока не придём к одному из нижерассмотренных ситуаций. Так как при этом мы работаем только с коэффициентами при неизвестных и свободными членами, то метод Гаусса можно свести к элементарным преобразованиям строк расширенной матрицы системы.
а) Оформим решение в виде элементарных преобразований расширенной матрицы системы:
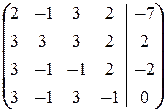
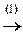
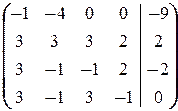
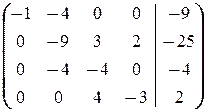
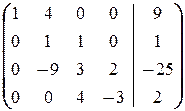
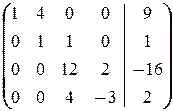
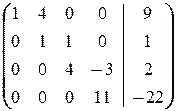
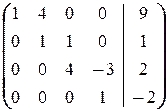
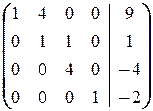
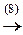
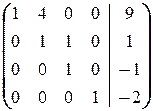

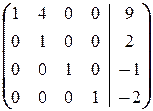
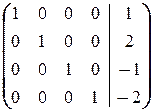
á(1) Из первой строки вычли вторую.
(2) 1-ю строку, умноженную на 3, прибавили ко 2-й; 2-ю вычли из 3-й; 3-ю вычли из 4-й. Таким образом, получили систему
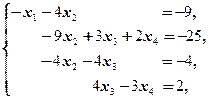
которая равносильна исходной системе. В ней из 3-го и 4-го уравнений исключена неизвестная x 1 (впрочем, оказалось, что из последнего исключена и x 2).
(3) 1-ю и 3-ю строки умножили на -1; поменяли местами 2-ю и 3-ю строки.
(4) 2-ю строку, умноженную на 9, прибавили к 3-й. Получили систему
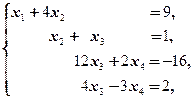
в которой из 3-го и 4-го уравнений кроме x 1 исключена неизвестная x 2.
(5) Последнюю строку, умноженную на 3, вычли из 3-й и поменяли их местами. Таким образом, исходную систему привели к треугольному виду:
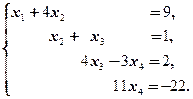
Теперь из последнего уравнения находим x 4, подставляя которое в 3-е, находим x 3 (ниже преобразования (7) и (8)), после чего из 2-го уравнения находим x 2 (преобразование (9)) и, наконец, из 1-го находим x 1 (преобразование (10)).
(6) Последнюю строку разделили на -11.
(7) Последнюю строку, умноженную на 3, прибавили к 3-й.
(8) 3-ю строку разделили на 4.
(9) 3-ю строку вычли из 2-й.
(10) 2-ю строку, умноженную на 4, вычли из 1-й.ñ
Следовательно, x 1=1, x 2=2, x 3= -1, x 4 = -2.
б) Аналогично предыдущему имеем
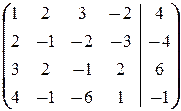
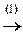
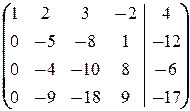
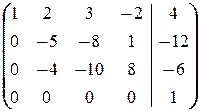
Последняя строка означает, что 0=1 ¾ противоречие. Значит, система несовместна.
á(1) 1-ю строку, умноженную на 2, на 3 и на 4, вычитаем из 2-й, 3-й и 4-й строк соответственно (исключили x 1 из 2-го, 3-го и 4-го уравнений).
(2) Сумму 2-й и 3-й строк вычитаем из 4-й.ñ
в)
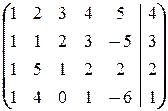
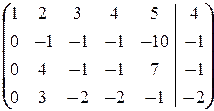
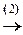
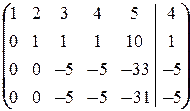
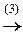
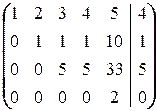
 Ä
Ä
á(1) 1-ю строку вычли из второй, вторую - из третьей и четвёртой; исключили из 2-го и остальных уравнений x 1.
(2) Умножая на 4 и 3, вторую строку прибавили соответственно к 3-й и 4-й; из 3-го и 4-го уравнений кроме x 1 исключили и x 2.
(3) Из 4-й строки вычли 3-ю и 3-ю умножили на -1; исключили из 4-го x 3, кроме того, исключилась и x 4.ñ
Таким образом, получили систему
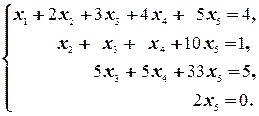
Пришли к системе «трапециедального» вида. В ней неизвестных больше, чем уравнений. Поэтому некоторые неизвестные выбираем связанными, а остальные ¾ свободными. Именно, связанные неизвестные ¾ это первые неисключённые неизвестные в уравнениях: x 1, x 2, x 3 и x 5. Неизвестная x 4 ¾ свободная.
Ä 
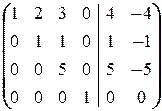
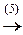
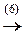
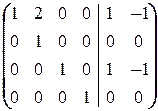
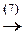
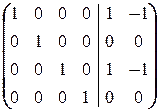
á(4) Свободной неизвестной придаём произвольное значение x 4= a и переносим в правую часть уравнений; из последнего уравнения находим x 5=0.
(5) 3-ю строку делим на 5.
(6) Из 2-й строки вычли 3-ю.
(7) 2-ю строку, умноженную на 2, вычли из 1-й.ñ
Таким образом, приходим к решению системы:
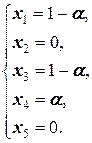
Получаем окончательно {1- a, 0, 1- a, a, 0) | a Î R }.
В частности, система неопределенная. Решаем ее методом Жордана-Гаусса. Решение также оформляем в виде элементарных преобразований расширенной матрицы:
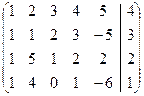
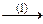
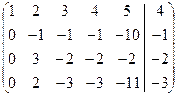
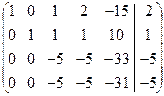
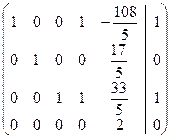
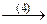
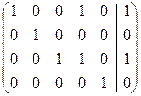
á(1) 1-ю строку вычли из остальных; исключили из 2-го и остальных уравнений неизвестную x 1.
(2) 2-ю строку умножили на -1, а затем новую 2-ю, умноженную на 2, вычли из 1-ой и 4-ой, и, умноженную на 3, вычли из 3-ей; исключили неизвестную x 2 из 1-го, 3-го и 4-го уравнений.
(3) 3-ю строку разделили на -5, а затем новую 3-ю вычли из первой и второй, и, умноженную на 5, прибавили к 4-ой; исключили неизвестную x 3 из 1-го, 2-го и 4-го уравнений.
(4) Последнюю строку разделили на 2, а затем ее, умноженную на 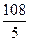 , прибавили к 1-ой, и, умноженную соответственно на
, прибавили к 1-ой, и, умноженную соответственно на 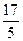 и
и 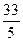 , вычли из 2-ой и 3-ей.ñ
, вычли из 2-ой и 3-ей.ñ
Таким образом, x 1, x 2, x 3 и x 5 - связанные (базисные) неизвестные, x 4 - свободная. Придавая последней произвольные значения a и перенося ее в правую часть, приходим к решению {(1- a, 0, 1- a, a, 0}| a Î R }.
Ответ: а) (1; 2; -1; -2);
б) Система несовместна;
в) {1- a, 0, 1- a, a, 0) | a Î R }.
2. Решить систему
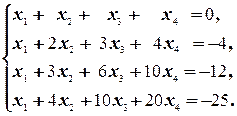
над полем R используя:
а) матричный метод;
б) правило Крамера.
Решение: Матричный метод решения систем заключается в том, что если определитель det A основной матрицы A системы, у которой число уравнений равно числу неизвестных, не равен нулю, то столбец X неизвестных ищется по формуле X = A 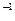 B, где B ¾ столбец неизвестных системы. Таким образом, действуем по следующей схеме:
B, где B ¾ столбец неизвестных системы. Таким образом, действуем по следующей схеме:
1) Находим det A, и если det A ¹0, то
2) Находим A 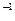 .
.
3) Находим X.
В нашем случае A = 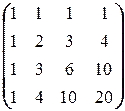 , B =
, B = 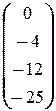 . Итак,
. Итак,
1) Находим det A.
det A ищем приведением к треугольному виду:
det A = 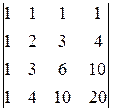
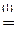
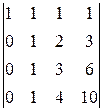
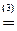
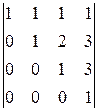
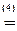 1.
1.
á(1) 1-ю строку вычли из остальных.
(2) 2-ю строку вычли из 3-й, 3-ю ¾ из 4-й.
(3) 3-ю строку вычли из 4-й.
(4) Теперь определитель треугольного вида равен произведению диагональных элементов.ñ
Таким образом, det A ¹0. Значит, A 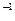 существует.
существует.
2) НаходимA 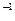 .
.
Найдем A 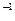 методом приписывания единичной матрицы:
методом приписывания единичной матрицы:
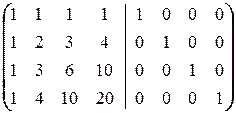
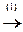
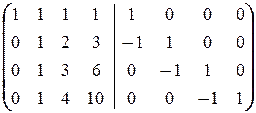
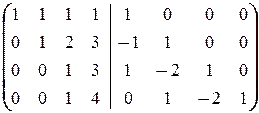
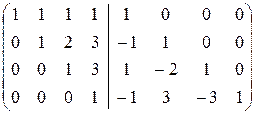
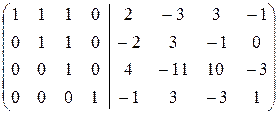
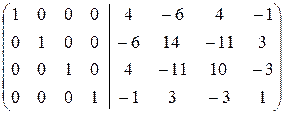
áПреобразования (1) ¾ (2) совпадают с соответствующими преобразованиями при нахождении det A.
(4) 4-ю строку, умноженную на 3, вычли из 3-й, 3-ю ¾ из 2-й, 4-ю ¾ из 1-й.
(5) 3-ю строку вычли из 2-й, 2-ю ¾ из 3-й, 3-ю ¾ из 2-й, 2-ю ¾ из 1-й.ñ
Таким образом, A 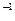 =
= 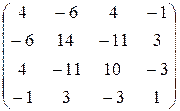
3) НаходимX:
X = 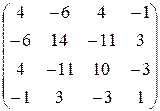 ×
× 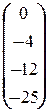 =
= 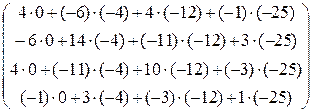 =
=  .
.
Таким образом, x 1=1, x 2=1, x 3= -1, x 4 = -1.
б) Правило Крамера заключается в том, что если определитель основной матрицы системы, у которой число уравнений равно числу неизвестных, не равен нулю, то решением системы является 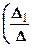 ,
, 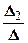 , …,
, …, 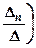 , где D=det A ¾ определитель системы, D i ¾ определитель, полученный из определителя D заменой i -го столбца на столбец свободных членов.
, где D=det A ¾ определитель системы, D i ¾ определитель, полученный из определителя D заменой i -го столбца на столбец свободных членов.
Как мы видели при решении системы матричным методом, D=1¹0, так что можно к системе применить правило Крамера.
Найдём D i для всех i =1, 2, 3, 4.
D1= 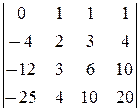
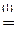
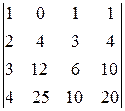
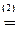
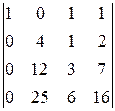
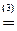
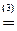 -
- 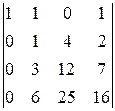
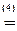 -
- 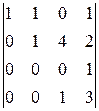
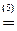
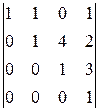 =1.
=1.
á(1) Из 1-го столбца вынесли знак «-» (знак определителя меняется на противоположный) и поменяли местами 1-й и 2-й столбцы (снова поменялся знак определителя на противоположный; в итоге знак перед определителем остаётся «+»).
(2) 1-ю строку, умноженную на 2, 3 и 4, вычли соответственно из 2-й, 3-й и 4-й строк.
(3) Поменяли местами 2-й и 3-й столбцы; знак определителя меняется на противоположный.
(4) 2-ю строку, умноженную на 3 и 6, вычли соответственно из 3-й и 4-й строк.
(5) Поменяли местами 3-ю и 4-ю строки.ñ
D2= 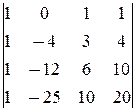
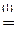
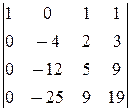
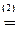
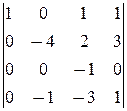
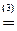
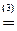 -
- 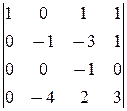
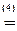 -
- 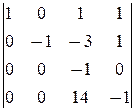
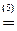 -
- 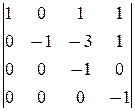 =1.
=1.
á(1) 1-ю строку вычли из остальных.
(2) 2-ю строку, умноженную на 3 и 6, вычли соответственно из 3-й и 4-й строк.
(3) Поменяли местами 2-ю и 4-ю строки.
(4) 2-ю строку, умноженную на 4, вычли из последней.
(5) 3-ю строку, умноженную на 14, прибавили к последней.ñ
D3= 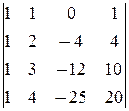
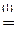
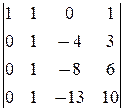
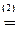
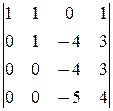
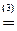
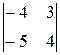 = -1.
= -1.
á(1) 1-ю строку вычли из 2-й, 2-ю ¾ из 3-й, 3-ю ¾ из 4-й.
(2) 2-ю строку вычли соответственно из 3-й и 4-й.
(3) Разложили определитель по первому столбцу, и полученный 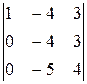 снова разложили по первому столбцу.ñ
снова разложили по первому столбцу.ñ
D4= 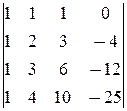 =
= 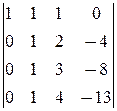 =
= 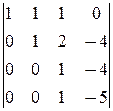 = -1.
= -1.
áD4 вычислили в точности так же, как и D3.ñ
Теперь находим x 1= 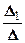 =
=  =1; x 2=
=1; x 2= 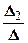 =
=  =-2; x 3=
=-2; x 3= 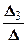 =
= 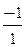 =-1; x 4=
=-1; x 4= 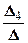 =
= 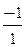 = -1.
= -1.
Ответ: (1; 1; -1; -1).
3. Исследовать систему на совместность и, в случае совместности, найти её решение в виде суммы частного и общего решения приведённой однородной:
а) 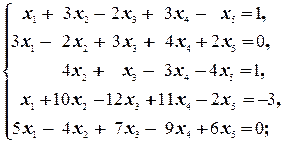 б)
б) 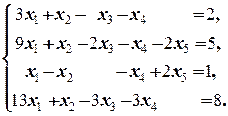
Решение. а) Исследуем систему на совместность. Система совместна тогда и только тогда, когда ранг матрицы A системы равен рангу её расширенной матрицы 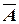 . Поэтому для исследования системы на совместность необходимо и достаточно нахождение рангов матрицы A системы и её расширенной
. Поэтому для исследования системы на совместность необходимо и достаточно нахождение рангов матрицы A системы и её расширенной 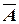 , а затем сравнить найденные ранги. Если ранги A и
, а затем сравнить найденные ранги. Если ранги A и 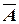 равны, то система совместна; в противном случае она не совместна.
равны, то система совместна; в противном случае она не совместна.
Ранги будем искать методом окаймления миноров. В нашем случае матрицы A и 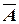 ¾ следующие:
¾ следующие:
A = 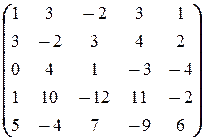 и
и 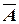 =
= 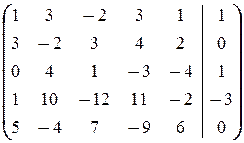 .
.
Среди миноров первого порядка матрицы есть ненулевой: M 1=1¹0. Он составлен из элемента 1-й строки и 1-го столбца. Окаймляем его 2-м столбцом и 2-й строкой: M 2= 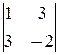 = -11¹0. Продолжаем окаймлять вновь полученные ненулевые миноры:
= -11¹0. Продолжаем окаймлять вновь полученные ненулевые миноры:
M 3= 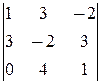 =-47¹0; M 4=
=-47¹0; M 4= 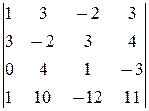
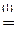
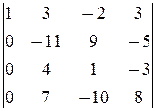
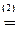 0.
0.
á(1) 1-ю строку, умноженную на 3 и 1, вычли соответственно из 2-й и 4-й.
(2) Так как сумма 3-й и 4-й строк, умноженная на -1, равна 2-й строке, то определитель равен 0.ñ
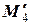 =
= 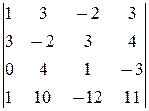
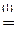
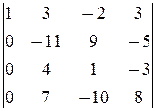
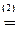 0.
0.
áАналогично M 4ñ
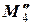 =
= 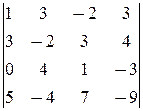
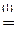
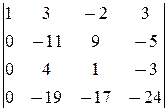
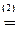
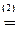
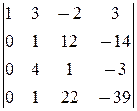
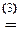
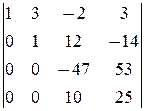
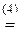
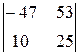 ¹0.
¹0.
á(1) 1-ю строку, умноженную на 3 и 5, вычли соответственно из 2-й и 4-й.
(2) 3-ю строку, умноженную на 3 и 5, прибавили соответственно ко 2-й и 4-й.
(3) 2-ю строку вычли из 4-й и, умноженную на 4, вычли из 2-й.
(4) Поступили точно так же, как и в (3) при вычислении D3 в предыдущем примере.ñ
Таким образом, максимальный порядок ненулевых миноров матрицы А равен 4, то есть rg А =4.
Для нахождения rg 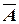 достаточно окаймить ненулевой минор
достаточно окаймить ненулевой минор 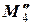 матрицы
матрицы 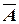 4-й строкой и столбцом свободных членов:
4-й строкой и столбцом свободных членов:
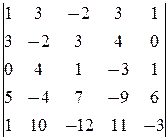
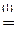
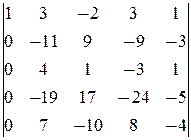
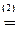
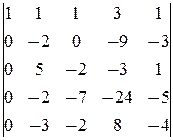
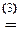
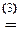 -
- 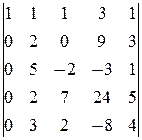
 -
-  ×
× 
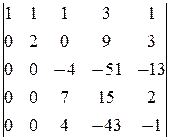
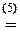
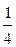
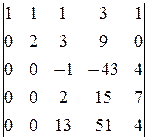
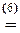
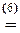
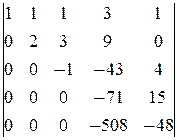
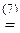
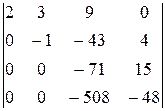
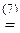
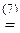 2×
2× 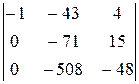
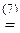 -2×
-2× 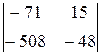 ¹ 0.
¹ 0.
á(1) 1-ю строку, умноженную на соответствующие коэффициенты, вычли из 2-й, 4-й и 5-й строк.
(2) Ко 2-му столбцу прибавили 3-й столбец, у 3-му ¾ 4-й.
(3) Из 2-го, 3-го и 4-го строк вынесли -1.
(4) 2-ю строку, умноженную на 5, вычли из 3-й, умноженной на 2; 2-ю вычли из 4-й; 2-ю, умноженную на 3, вычли из 5-й, умноженной на 2.
(5) Вынесли «-» из 3-й строки и поменяли местами сначала 3-ю и 5-ю строки, затем 3-й и 5-й столбцы.
(6) 3-ю строку, умноженную на 2 и 13, прибавили соответственно к 4-й и 5-й строке.
(7) Разлагаем определители по первому столбцу.ñ
Получаем, что rg 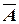 =5, то есть rg А ¹ rg
=5, то есть rg А ¹ rg 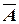 и система несовместна.
и система несовместна.
б) Исследуем систему на совместность (по-прежнему, методом окаймления миноров). Имеем:
A = 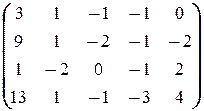 и
и 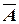 =
= 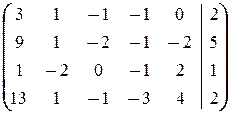 .
.
Поэтому
M 1=3¹0, M 2= 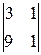 = -6¹0, M 3=
= -6¹0, M 3= 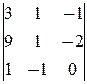
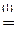
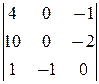
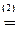 (-1)×(-1)3+1
(-1)×(-1)3+1 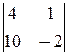 =2¹0.
=2¹0.
á(1) Последнюю строку прибавили к 1-й и 2-й.
(2) Разложили определитель по 2-му столбцу.ñ
M 4= 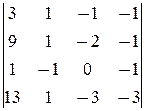 =0,
=0, 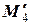 =
= 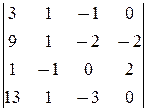 =0.
=0.
Таким образом, rg А =3.
Так как 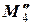 =
= 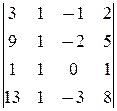 =0, то rg
=0, то rg 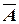 =3 и ¾ rg А = rg
=3 и ¾ rg А = rg 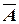 система совместна.
система совместна.
áВо всех определителях M 4, 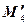 ,
, 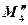 и последняя строка равна сумме первых трёхñ
и последняя строка равна сумме первых трёхñ
Далее, исходная система равносильна системе
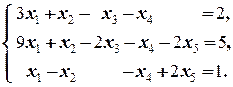 (*)
(*)
Так как минор третьего порядка, составленный из коэффициентов при x 1, x 2 и x 3, не равен нулю, то x 4 и x 5 ¾ свободные неизвестные.
Теперь действуем по следующей схеме:
1) Находим общее решение однородной приведённой системы (*).
2) Находим частное решение системы.
3) Составляем общее решение исходной системы в виде суммы частного решения системы (*) и общего решения однородной приведённой системы(*).
1) Выпишем однородную приведённую системы (*):
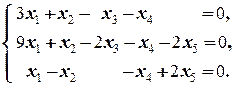
Положим x 4=1, x 5=0. Получаем систему
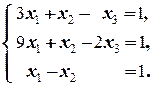
 Ä
Ä
Для её решения применим метод Гаусса
Ä 
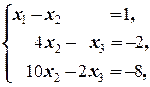
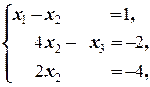
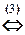
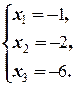
Таким образом, первый фундаментальный вектор однородной приведённой системы ¾ e 1=(-1; -2; -6; 1; 0).
á(1) Исключили из 1-го и 2-го уравнений x 1.
(2) Из 3-го уравнения исключили x 3.
(3) Последовательно находим x 2, x 3 и x 1.ñ
Положим x 4=0, x 5=1. Получаем систему
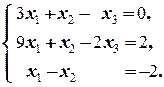 Û Ä
Û Ä
Снова применяем метод Гаусса:
Ä Û 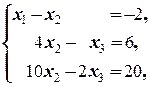 Û
Û 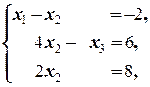 Û
Û 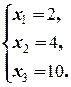
Таким образом, второй фундаментальный вектор однородной системы ¾ e 2=(2; 4; 10; 0; 1).
áСистема решена аналогичными преобразованиями, как и в предыдущей системеñ.
Находим общее решение однородной приведённой
X 0= ae 1+ be 2= a (-1; -2; -6; 1; 0)+ b (2; 4; 10; 0; 1)=(- a +2 b; -2 a +4 b; -6 a +10 b; a; b).
2) Положив x 4= x 5=0, находим частное решение неоднородной (*):
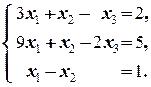 Û
Û 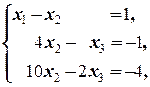 Û
Û 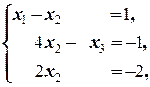 Û
Û 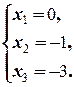
Таким образом, частное решение исходной системы ¾ Xч =(0; -1; -3; 0; 0).
3) Найдём общее решение исходной системы.
Xн =(0; -1; -3; 0; 0)+(- a +2 b; -2 a +4 b; -6 a +10 b; a; b)=
=(- a +2 b; -1-2 a +4 b; -3-6 a +10 b; a; b).
Ответ: а) Система несовместна.
б) Система совместна. Общее решение имеет вид (- a +2 b; -1-2 a +4 b; -3-6 a +10 b; a; b), где a, b любые числа.
Приложение 3. Некоторые понятия и факты высшей алгебры.
 2015-03-08
2015-03-08 1889
1889
