2.3.1. Теорема (Кронекера-Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу её расширенной матрицы.
2.3.2. Упражнение. Исследовать систему на совместность и в случае совместности решить её методом Гаусса:
а) 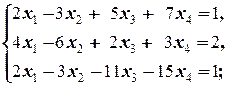 б)
б) 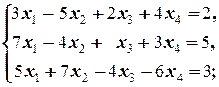
в) 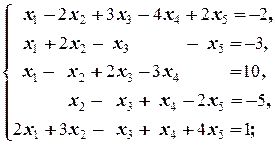 г)
г) 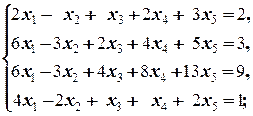
д) 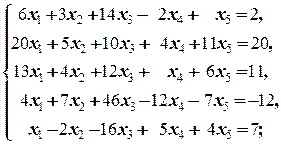 е)
е) 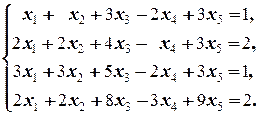
Решение. а) Найдём ранги обеих матриц (основной и расширенной) методом окаймления миноров, предварительно выписав основную и расширенную матрицы системы:
A = 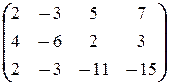 и
и 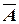 =
= 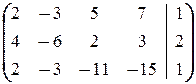
Найдём ранг основной матрицы:
M 1=2¹0, M 2= 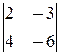 =0,
=0, 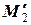 =
= 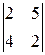 = -16¹0, M 3=
= -16¹0, M 3= 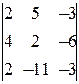 =0,
=0, 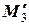 =
= 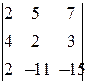 =0. Таким образом, rg A =2.
=0. Таким образом, rg A =2.
Для нахождения ранга расширенной матрицы достаточно окаймить ненулевой минор 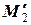 максимального порядка матрицы A 3-й строкой и столбцом свободных членов, так как все миноры матрицы A являются также минорами матрицы
максимального порядка матрицы A 3-й строкой и столбцом свободных членов, так как все миноры матрицы A являются также минорами матрицы 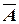 :
: 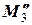 =
= 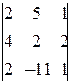 =0. Следовательно, rg
=0. Следовательно, rg 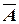 = rg A =2 и система совместна.
= rg A =2 и система совместна.
Решаем систему эквивалентными преобразованиями расширенной матрицы:
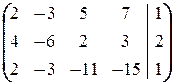 ®
® 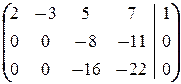 ®
® 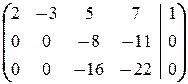 ® Ä
® Ä
(в частности получаем ещё раз, что ранг расширенной матрицы равен 2)
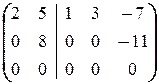 ®
® 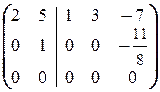 ®
®
® 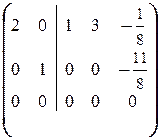 ®
®  .
.
Таким образом, x 1= 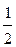 +
+ 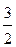 a -
a - 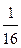 b, x 2= a, x 3=-
b, x 2= a, x 3=- 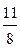 b, x 4= b.
b, x 4= b.
б) M 1=3¹0, M 2= 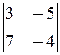 =23¹0, M 3=
=23¹0, M 3= 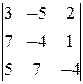 =0,
=0, 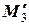 =
= 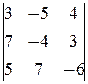 =0. Таким образом, rg A =2. Далее,
=0. Таким образом, rg A =2. Далее, 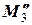 =
= 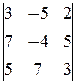 = -33¹0, то есть rg
= -33¹0, то есть rg 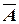 =3. Так как rg A ¹ rg
=3. Так как rg A ¹ rg 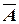 , то система несовместна.
, то система несовместна.
Ответ: а) (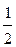 +
+ 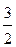 a -
a - 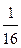 b; a; -
b; a; - 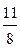 b; b), где a, b Î R;
b; b), где a, b Î R;
б) Система несовместна.
 2015-03-08
2015-03-08 1032
1032








