Если неизвестная функция 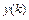 и заданная функция
и заданная функция 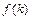 являются функциями одного целочисленного аргумента
являются функциями одного целочисленного аргумента 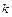 , то уравнение вида
, то уравнение вида 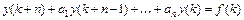 ,
, 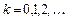 , где
, где 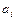
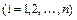 - постоянные коэффициенты, называется линейным разностным уравнением ( ЛРУ )
- постоянные коэффициенты, называется линейным разностным уравнением ( ЛРУ ) 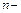 го порядка с постоянными коэффициентами. Если
го порядка с постоянными коэффициентами. Если 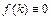 , то уравнение называется однородным.
, то уравнение называется однородным.
Функция 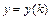 ,
, 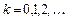 , обращающая разностное уравнение в тождество, называется его решением.
, обращающая разностное уравнение в тождество, называется его решением.
Условия 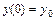 ,
, 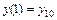 ,…,
,…, 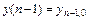 , где
, где 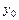 ,
, 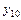 ,…,
,…, 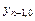 - заданные числа, называются начальными условиями.
- заданные числа, называются начальными условиями.
Общим решением РУ 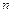 -го порядка называется решение
-го порядка называется решение 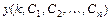 , зависящее от
, зависящее от 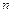 произвольных постоянных
произвольных постоянных 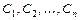 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных  можно получить решение
можно получить решение 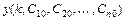 , удовлетворяющее заданным начальным условиям
, удовлетворяющее заданным начальным условиям 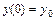 ,
, 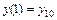 ,…,
,…, 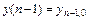 . Частным решением называется решение
. Частным решением называется решение 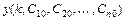 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных  .
.
Общее решение однородного ЛРУ 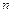 -го порядка
-го порядка 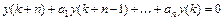 ищется, аналогично общему решению дифференциального уравнения
ищется, аналогично общему решению дифференциального уравнения 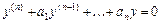 , в виде
, в виде 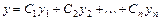 , где
, где 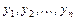 - фундаментальная система его решений;
- фундаментальная система его решений; 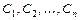 - произвольные постоянные.
- произвольные постоянные.
Фундаментальной системой решений однородного ЛРУ  -го порядка
-го порядка 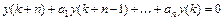 называется любая система из
называется любая система из  линейно независимых частных решений
линейно независимых частных решений 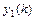 ,
, 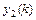 ,…,
,…, 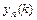 этого уравнения.
этого уравнения.
Фундаментальная система решений 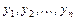 строится на основе характера корней характеристического уравнения
строится на основе характера корней характеристического уравнения 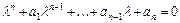 . А именно: 1) если
. А именно: 1) если 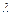 - действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение
- действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение 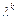 разностного уравнения; 2) если
разностного уравнения; 2) если 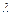 - действительный корень кратности
- действительный корень кратности 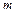 , то ему в ФСР соответствует
, то ему в ФСР соответствует 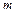 линейно независимых частных решений:
линейно независимых частных решений: 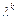 ,
, 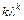 ,
, 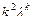 ,…,
,…, 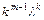 ; 3) если
; 3) если 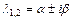 - пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения:
- пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения: 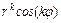 ,
, 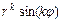 , где
, где 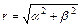 ,
, 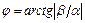 .
.
Общее решение неоднородного линейного разностного уравнения 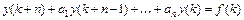 имеет вид
имеет вид 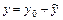 , где
, где 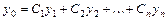 - общее решение соответствующего однородного разностного уравнения,
- общее решение соответствующего однородного разностного уравнения, 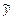 - какое-нибудь частное решение данного неоднородного уравнения.
- какое-нибудь частное решение данного неоднородного уравнения.
Как и в случае дифференциальных уравнений, частное решение 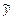 разностного уравнения с правой частью специального вида
разностного уравнения с правой частью специального вида 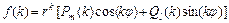 ищется методом неопределённых коэффициентов в виде
ищется методом неопределённых коэффициентов в виде 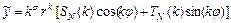 , где
, где 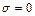 , если число
, если число 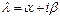 , для которого
, для которого 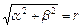 и
и 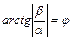 , не является корнем характеристического уравнения, и
, не является корнем характеристического уравнения, и 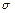 равно кратности корня
равно кратности корня 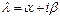 в противном случае;
в противном случае; 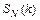 и
и 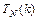 - полные многочлены степени
- полные многочлены степени 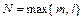 с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени
с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени 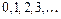 соответственно являются:
соответственно являются: 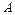 ,
, 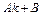 ,
, 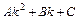 ,
, 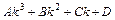 ,…. Для нахождения коэффициентов многочленов
,…. Для нахождения коэффициентов многочленов 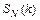 и
и 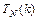 , надо подставить решение
, надо подставить решение 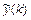 в неоднородное разностное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
в неоднородное разностное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
В задачах 9.281-9.288 найти общие решения следующих однородных разностных уравнений:
9.281 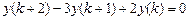 .
.
9.282 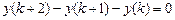 .
.
9.283 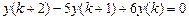 .
.
9.284 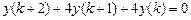 .
.
9.285 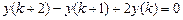 .
.
9.286 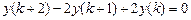 .
.
9.287 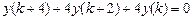 .
.
9.288 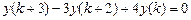 .
.
В задачах 9.289-9.292 найти частные решения разностных уравнений, удовлетворяющие указанным начальным условиям:
9.289 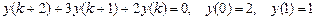 .
.
9.290 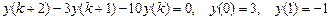 .
.
9.291 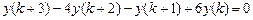 ,
,
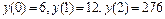 .
.
9.292 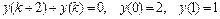 .
.
В задачах 9.293-9.308 найти общие решения следующих неоднородных разностных уравнений
9.293 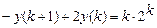 .
.
9.294 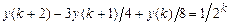 .
.
9.295 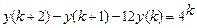 .
.
9.296 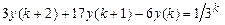 .
.
9.297 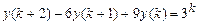 .
.
9.298 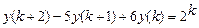 .
.
9.299  .
.
9.300 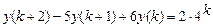 .
.
9.301 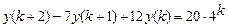 .
.
9.302 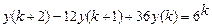 .
.
9.303 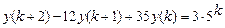 .
.
9.304 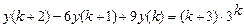 .
.
9.305 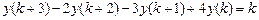 .
.
9.306 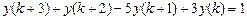 .
.
9.307 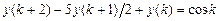 .
.
9.308 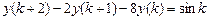 .
.
В задачах 9.309-9.312 найти частные решения разностных уравнений, удовлетворяющие указанным начальным условиям:
9.309 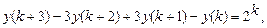
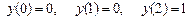 .
.
9.310 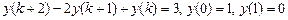 .
.
9.311 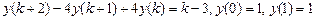 .
.
9.312 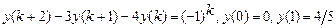 .
.
По аналогии с нормальными системами дифференциальных уравнений рассматриваются также и нормальные системы разностных уравнений вида 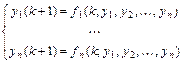 , где
, где 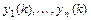 - искомые функции,
- искомые функции, 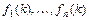 - заданные функции целочисленного аргумента
- заданные функции целочисленного аргумента 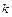 ,
, 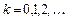 . Число
. Число 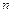 называется порядком системы. Совокупность
называется порядком системы. Совокупность 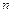 функций
функций 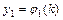 ,
, 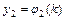 ,…,
,…, 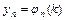 обращающих каждое уравнение системы в тождество, называется решением этой системы.
обращающих каждое уравнение системы в тождество, называется решением этой системы.
Условия 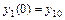 ,
, 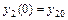 ,…,
,…, 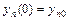 , где
, где 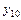 ,
, 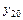 ,…,
,…, 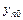 - заданные числа, называются начальными условиями.
- заданные числа, называются начальными условиями.
Общим решением системы РУ 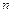 -го порядка называется решение:
-го порядка называется решение:
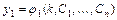 ,
, 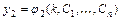 ,…,
,…, 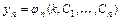 ,
,
зависящее от 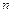 произвольных постоянных
произвольных постоянных 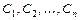 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных 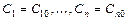 можно получить решение, удовлетворяющее заданным начальным условиям
можно получить решение, удовлетворяющее заданным начальным условиям 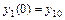 ,
, 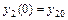 ,…,
,…, 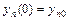 .
.
Частным решением системы называется решение 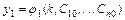 ,
, 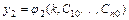 ,…,
,…, 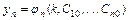 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных  .
.
Нормальные системы разностных уравнений аналогично системам дифференциальных уравнений можно решать методом исключения неизвестных функций приводя их к одному разностному уравнению 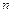 -го порядка. Для нахождения решения, например, системы двух разностных уравнений
-го порядка. Для нахождения решения, например, системы двух разностных уравнений 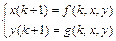 , где
, где 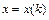 ,
, 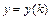 - неизвестные функции целочисленного аргумента
- неизвестные функции целочисленного аргумента 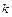 поступают следующим образом. Сначала, используя первое из уравнений системы, получим уравнение
поступают следующим образом. Сначала, используя первое из уравнений системы, получим уравнение 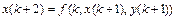 , в которое затем подставим второе уравнение системы
, в которое затем подставим второе уравнение системы 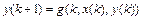 , с учётом выражения
, с учётом выражения 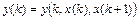 , найденного из первого уравнения системы. В результате получим разностное уравнение 2-го порядка относительно неизвестной функции
, найденного из первого уравнения системы. В результате получим разностное уравнение 2-го порядка относительно неизвестной функции 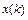 , решив которое найдём функцию
, решив которое найдём функцию 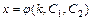 , где
, где 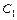 ,
, 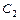 - произвольные постоянные. Подставив
- произвольные постоянные. Подставив 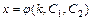 в формулу
в формулу 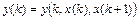 , определим функцию
, определим функцию 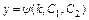 . Совокупность функций
. Совокупность функций 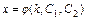 ,
, 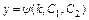 даёт общее решение системы.
даёт общее решение системы.
В задачах 9.313-9.320 найти методом исключения решения следующих систем разностных уравнений:
9.313 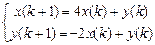 . 9.314
. 9.314 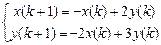 .
.
9.315 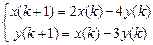 . 9.316
. 9.316 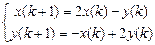 .
.
9.317 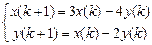 . 9.318
. 9.318 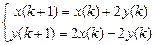 .
.
9.319 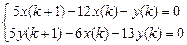 .
.
9.320 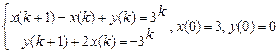 .
.
 2015-03-20
2015-03-20 1256
1256
