Уравнение вида 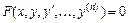 , где
, где 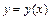 - искомая функция, называется дифференциальным уравнением
- искомая функция, называется дифференциальным уравнением 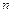 -го порядка. Функция
-го порядка. Функция 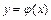 , обращающая уравнение в тождество, называется решением уравнения, а график этой функции – интегральной кривой. Если решение уравнения задано в неявном виде
, обращающая уравнение в тождество, называется решением уравнения, а график этой функции – интегральной кривой. Если решение уравнения задано в неявном виде 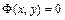 , то оно называется интегралом уравнения.
, то оно называется интегралом уравнения.
Уравнение вида 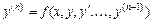 , называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ
, называется уравнением, разрешённым относительно старшей производной. Эту форму записи ДУ 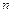 -го порядка называют нормальной.
-го порядка называют нормальной.
Условия 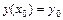 ,
, 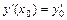 ,…,
,…, 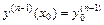 , где
, где 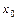 ,
, 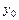 ,
, 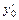 ,…,
,…, 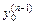 - заданные числа, называются начальными условиями. Задача нахождения решения уравнения
- заданные числа, называются начальными условиями. Задача нахождения решения уравнения 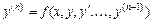 , удовлетворяющего заданным начальным условиям, называется задачей Коши.
, удовлетворяющего заданным начальным условиям, называется задачей Коши.
Общим решением ДУ 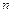 -го порядка называется решение
-го порядка называется решение 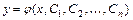 , зависящее от
, зависящее от 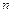 произвольных постоянных
произвольных постоянных 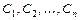 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных  можно получить решение
можно получить решение 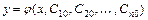 , удовлетворяющее заданным начальным условиям
, удовлетворяющее заданным начальным условиям 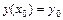 ,
, 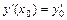 ,…,
,…, 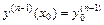 . Общее решение, заданное в неявном виде
. Общее решение, заданное в неявном виде 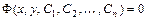 , называется общим интегралом уравнения.
, называется общим интегралом уравнения.
Частным решением ДУ 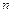 -го порядка называется решение
-го порядка называется решение 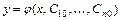 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных 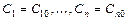 . Частное решение, заданное в неявном виде
. Частное решение, заданное в неявном виде 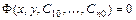 , называется частным интегралом уравнения.
, называется частным интегралом уравнения.
Если для искомого частного решения 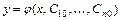 уравнения
уравнения 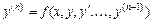 заданы начальные условия
заданы начальные условия 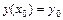 ,
, 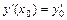 ,…,
,…, 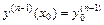 и известно общее решение
и известно общее решение 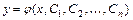 уравнения, то значения
уравнения, то значения 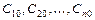 произвольных постоянных определяются, если это возможно, из системы уравнений
произвольных постоянных определяются, если это возможно, из системы уравнений 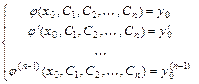 .
.
Уравнение вида 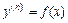 называется простейшим дифференциальным уравнением
называется простейшим дифференциальным уравнением 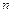 -го порядка. Его общее решение находят, выполняя последовательно
-го порядка. Его общее решение находят, выполняя последовательно 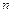 интегрирований, и записывают в виде
интегрирований, и записывают в виде
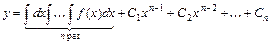 .
.
Уравнение вида 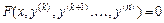 ,
, 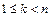 , не содержащее явно искомой функции
, не содержащее явно искомой функции 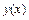 , с помощью подстановки
, с помощью подстановки 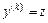 , где
, где 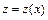 - новая неизвестная функция, приводится к уравнению
- новая неизвестная функция, приводится к уравнению 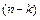 порядка
порядка 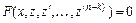 .
.
Уравнение вида 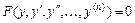 , не содержащее явно независимой переменной
, не содержащее явно независимой переменной 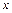 , с помощью подстановки
, с помощью подстановки 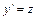 , где
, где  - новая неизвестная функция от новой независимой переменной
- новая неизвестная функция от новой независимой переменной 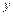 , приводится к уравнению порядка на единицу ниже. При этом
, приводится к уравнению порядка на единицу ниже. При этом 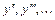 преобразуются так:
преобразуются так: 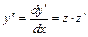 ,
,  ,…..
,…..
В задачах 9.131-9.150 найти общие решения дифференциальных уравнений,допускающих понижение порядка:
9.131 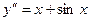 . 9.132
. 9.132 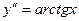 . 9.133
. 9.133 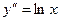 .
.
9.134 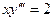 . 9.135
. 9.135 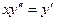 . 9.136
. 9.136 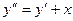 .
.
9.137 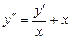 . 9.138
. 9.138 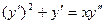 .
.
9.139 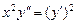 . 9.140
. 9.140 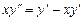 .
.
9.141 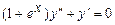 . 9.142
. 9.142 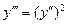 .
.
9.143 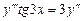 . 9.144
. 9.144 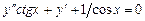 .
.
9.145 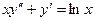 . 9.146
. 9.146 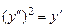 .
.
9.147 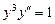 . 9.148
. 9.148 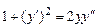 .
.
9.149 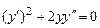 . 9.150
. 9.150 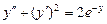 .
.
В задачах 9.151-9.160 найти частные решения следующих уравнений при указанных начальных условиях:
9.151 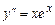 ,
, 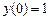 ,
, 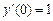 .
.
9.152 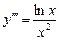 ,
, 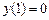 ,
, 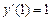 ,
, 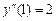 .
.
9.153 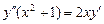 ,
, 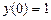 ,
, 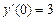 .
.
9.154 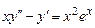 ,
, 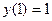 ,
, 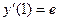 .
.
9.155 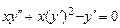 ,
, 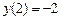 ,
, 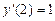 .
.
9.156 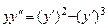 ,
, 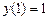 ,
, 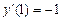 .
.
9.157 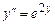 ,
, 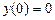 ,
, 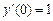 .
.
9.158 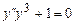 ,
, 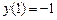 ,
, 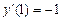 .
.
9.159 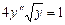 ,
, 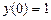 ,
, 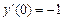 .
.
9.160 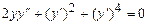 ,
, 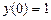 ,
, 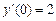 .
.
Функции 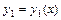 ,
, 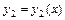 ,…,
,…, 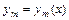 называются линейно зависимыми на
называются линейно зависимыми на 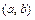 , если существуют постоянные
, если существуют постоянные 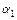 ,
, 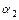 ,…,
,…, 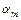 , не все равные нулю, такие, что
, не все равные нулю, такие, что 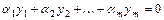 для всех
для всех 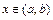 . Если равенство выполняется для всех
. Если равенство выполняется для всех 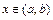 только при условии
только при условии 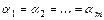 , то данные функции называются линейно независимыми на
, то данные функции называются линейно независимыми на 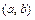 .
.
Определитель 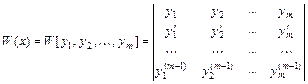 называется определителем Вронского (вронскианом).
называется определителем Вронского (вронскианом).
Если функции 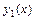 ,
, 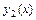 ,…,
,…, 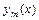 линейно зависимы на
линейно зависимы на 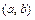 , то определитель Вронского
, то определитель Вронского 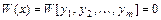 для всех
для всех 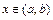 (необходимое условие линейной зависимости).
(необходимое условие линейной зависимости).
Если 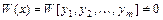 хотя бы в одной точке
хотя бы в одной точке 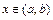 , то функции
, то функции 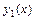 ,
, 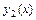 ,…,
,…, 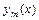 линейно независимы на
линейно независимы на 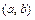 (достаточное условие линейной независимости).
(достаточное условие линейной независимости).
В задачах 9.161-9.170 исследовать, являются ли данные функции линейно независимыми (в каждой задаче функции рассматриваются в той области, в которой они все определены).
9.161 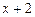 ,
, 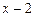 . 9.162
. 9.162 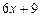 ,
, 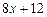 .
.
9.163 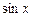 ,
, 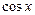 . 9.164
. 9.164 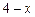 ,
, 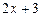 ,
, 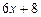 .
.
9.165 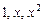 . 9.166
. 9.166 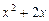 ,
, 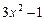 ,
, 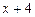 . 9.167
. 9.167 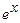 ,
, 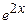 ,
, 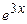 . 9.168
. 9.168 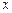 ,
, 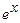 ,
, 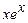 . 9.169
. 9.169 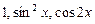 . 9.170
. 9.170 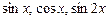 .
.
Уравнение вида 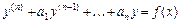 называется линейным дифференциальным уравнением ( ЛДУ )
называется линейным дифференциальным уравнением ( ЛДУ ) 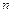 -го порядка, где коэффициенты
-го порядка, где коэффициенты  - непрерывные функции или постоянные. Если
- непрерывные функции или постоянные. Если 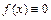 , то уравнение называется однородным. Однородное линейным уравнение
, то уравнение называется однородным. Однородное линейным уравнение 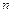 -го порядка имеет вид
-го порядка имеет вид 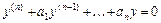 .
.
Любая система из 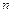 линейно независимых частных решений
линейно независимых частных решений 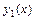 ,
, 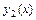 ,…,
,…, 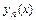 однородного линейного уравнения называется фундаментальной системой его решений.
однородного линейного уравнения называется фундаментальной системой его решений.
Общее решение однородного линейного уравнения 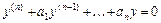 имеет вид
имеет вид 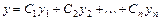 , где
, где 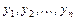 - фундаментальная система его решений;
- фундаментальная система его решений; 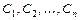 - произвольные постоянные.
- произвольные постоянные.
Фундаментальная система решений 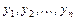 однородного ЛДУ с постоянными коэффициентами
однородного ЛДУ с постоянными коэффициентами 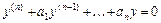 строится на основе характера корней характеристического уравнения
строится на основе характера корней характеристического уравнения 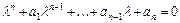 .
.
А именно: 1) если 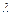 - действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение
- действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение 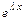 дифференциального уравнения; 2) если
дифференциального уравнения; 2) если 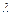 - действительный корень кратности
- действительный корень кратности 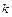 , то ему в ФСР соответствует
, то ему в ФСР соответствует 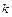 линейно независимых частных решений:
линейно независимых частных решений: 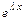 ,
,  ,
,  ,…,
,…, 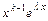 ; 3) если
; 3) если 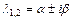 - пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения:
- пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения: 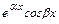 ,
, 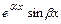 ; 4) если
; 4) если 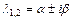 - пара комплексно-сопряжённых корней кратности
- пара комплексно-сопряжённых корней кратности 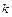 , то ей в ФСР соответствует
, то ей в ФСР соответствует 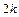 линейно независимых частных решений:
линейно независимых частных решений: 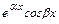 ,
, 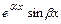 ,
, 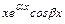 ,
, 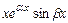 ,
, 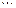 ,
, 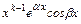 ,
, 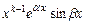 .
.
В задачах 9.171-9.184 найти общие решения однородных линейных дифференциальных уравнений с постоянными коэффициентами:
9.171 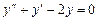 . 9.172
. 9.172 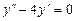 .
.
9.173 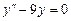 . 9.174
. 9.174 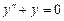 .
.
9.175 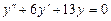 . 9.176
. 9.176 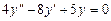 .
.
9.177 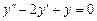 . 9.178
. 9.178 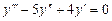 .
.
9.179 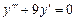 . 9.180
. 9.180 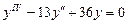 .
.
9.181 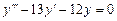 . 9.182
. 9.182 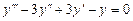 . 9.183
. 9.183 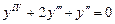 . 9.184
. 9.184 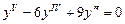 .
.
В задачах 9.185-9.188 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
9.185 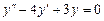 ,
, 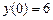 ,
, 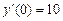 .
.
9.186 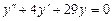 ,
, 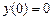 ,
, 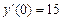 .
.
9.187 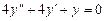 ,
, 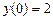 ,
, 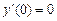 .
.
9.188 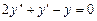 ,
, 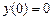 ,
,  .
.
Общее решение неоднородного ЛДУ 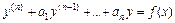 имеет вид
имеет вид 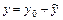 , где
, где 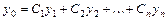 - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения, 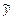 - какое-нибудь частное решение данного неоднородного уравнения.
- какое-нибудь частное решение данного неоднородного уравнения.
Частное решение 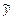 уравнения с правой частью специального вида
уравнения с правой частью специального вида 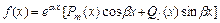 ищется методом неопределённых коэффициентов в виде
ищется методом неопределённых коэффициентов в виде 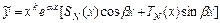 , где
, где 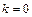 , если число
, если число 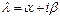 не является корнем характеристического уравнения, и
не является корнем характеристического уравнения, и 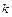 равно кратности корня
равно кратности корня 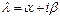 в противном случае;
в противном случае; 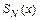 и
и 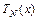 - полные многочлены степени
- полные многочлены степени 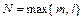 с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени
с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени 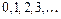 соответственно являются:
соответственно являются: 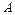 ,
, 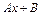 ,
, 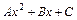 ,
, 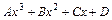 ,…. Для нахождения коэффициентов многочленов
,…. Для нахождения коэффициентов многочленов 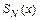 и
и 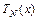 , надо подставить решение
, надо подставить решение 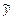 в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
в неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
Частное решение 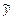 неоднородного ЛДУ с правой частью
неоднородного ЛДУ с правой частью 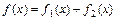 равно сумме частных решений
равно сумме частных решений 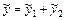 неоднородных уравнений с той же левой частью и правыми частями
неоднородных уравнений с той же левой частью и правыми частями 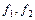 (принцип наложения решений).
(принцип наложения решений).
Частное решение 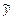 уравнения с любой правой частью
уравнения с любой правой частью 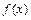 может быть найдено методом вариации произвольных постоянных. Для дифференциального уравнения второго порядка
может быть найдено методом вариации произвольных постоянных. Для дифференциального уравнения второго порядка 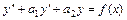 метод состоит в следующем. Если известна фундаментальная система решений
метод состоит в следующем. Если известна фундаментальная система решений 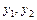 однородного уравнения
однородного уравнения 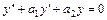 , то частное решение соответствующего неоднородного уравнения ищется в виде
, то частное решение соответствующего неоднородного уравнения ищется в виде 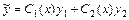 , где неизвестные функции
, где неизвестные функции 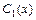 ,
, 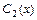 определяются из системы уравнений
определяются из системы уравнений 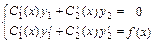 .
.
В задачах 9.189-9.202 для каждого из неоднородных линейных дифференциальных уравнений с постоянными коэффициентами написать общие решения уравнений (числовых значений коэффициентов в частных решениях не находить):
9.189 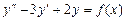 , если:
, если:
а) 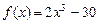 ; б)
; б) 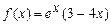 ;
;
в) 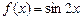 ; г)
; г) 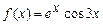 .
.
9.190 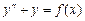 , если:
, если:
а) 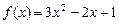 ; б)
; б) 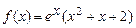 ;
;
в) 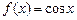 ; г)
; г) 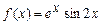 .
.
9.191 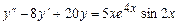 .
.
9.192 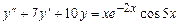 . 9.193
. 9.193 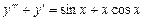 .
.
9.194 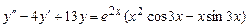 .
.
9.195 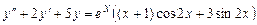 .
.
9.196 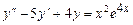 . 9.197
. 9.197 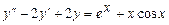 .
.
9.198 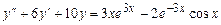 .
.
9.199 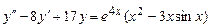 .
.
9.200 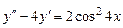 .
.
9.201 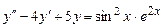 . 9.202
. 9.202 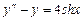 .
.
В задачах 9.203-9.212 для каждого из неоднородных линейных дифференциальных уравнений с постоянными коэффициентами найти их общие решения:
9.203  . 9.204
. 9.204 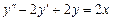 .
.
9.205 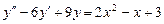 . 9.206
. 9.206 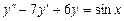 .
.
9.207 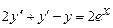 . 9.208
. 9.208 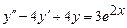 .
.
9.209 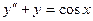 . 9.210
. 9.210 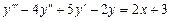 .
.
9.211 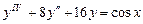 . 9.212
. 9.212 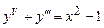 .
.
В задачах 9.213-9.218 найти частные решения уравнений, удовлетворяющих указанным начальным условиям:
9.213 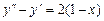 ,
, 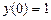 ,
, 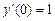 .
.
9.214 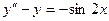 ,
, 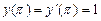 .
.
9.215 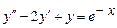 ,
, 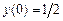 ,
, 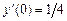 .
.
9.216 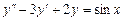 ,
, 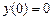 ,
, 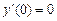 .
.
9.217 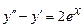 ,
, 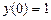 ,
, 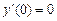 .
.
9.218 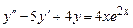 ,
, 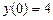 ,
, 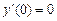 .
.
В задачах 9.219-9.228 найти общие решения неоднородных уравнений методом вариации произвольных постоянных:
9.219 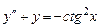 . 9.220
. 9.220 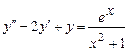 .
.
9.221 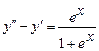 . 9.222
. 9.222 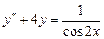 .
.
9.223 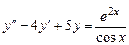 . 9.224
. 9.224 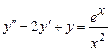 .
.
9.225 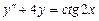 . 9.226
. 9.226 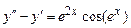 .
.
9.227 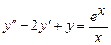 . 9.228
. 9.228 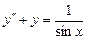 .
.
В задачах 9.229-9.244 найти общие решения следующих дифференциальных уравнений 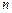 -ого порядка:
-ого порядка:
9.229 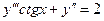 . 9.230
. 9.230 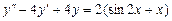 .
.
9.231 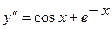 . 9.232
. 9.232 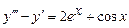 .
.
9.233 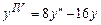 . 9.234
. 9.234 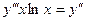 .
.
9.235 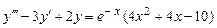 . 9.236
. 9.236 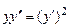 .
.
9.237 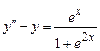 . 9.238
. 9.238 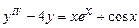 .
.
9.239 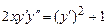 . 9.240
. 9.240 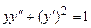 .
.
9.241 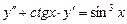 . 9.242
. 9.242 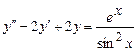 .
.
9.243 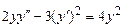 . 9.244
. 9.244 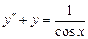 .
.
 2015-03-20
2015-03-20 441
441








