Замкнутую область 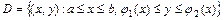 , где функции
, где функции 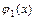 ,
, 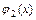 - непрерывны и заданы одним аналитическим выражением на отрезке
- непрерывны и заданы одним аналитическим выражением на отрезке 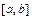 , будем называть элементарной в направлении оси
, будем называть элементарной в направлении оси 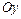 и обозначать
и обозначать 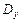 .
.
Замкнутую область 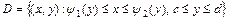 , где функции
, где функции 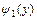 ,
, 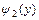 - непрерывны и заданы одним аналитическим выражением на отрезке
- непрерывны и заданы одним аналитическим выражением на отрезке 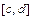 , будем называть элементарной в направлении оси
, будем называть элементарной в направлении оси 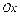 и обозначать
и обозначать 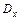 .
.
Область, элементарная в направлении одной из осей, не обязана быть элементарной в направлении другой.
Выражение 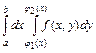 называется повторным интегралом от функции
называется повторным интегралом от функции 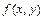 по области
по области 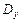 , а выражение
, а выражение 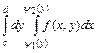 называется повторным интегралом от функции
называется повторным интегралом от функции 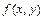 по области
по области 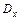 .
.
В повторных интегралах сначала вычисляются внутренние интегралы, причём интегрирование производится по внутренней переменной, а внешняя переменная считается постоянной. В результате получится подынтегральная функция для внешнего интеграла, интегрируя которую получим число.
В задачах 10.1-10.8 вычислить повторные интегралы:
10.1 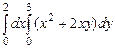 . 10.2
. 10.2 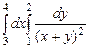 .
.
10.3 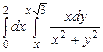 . 10.4
. 10.4 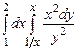 .
.
10.5 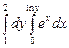 . 10.6
. 10.6 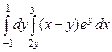 .
.
 2015-03-20
2015-03-20 437
437







