Дифференциальным уравнением в частных производных называется равенство, содержащее неизвестную функцию от нескольких независимых переменных, сами независимые переменные и частные производные неизвестной функции по независимым переменным. Порядок старшей частной производной называется порядком уравнения. Функция, обращающая уравнение в тождество, называется решением уравнения. Процесс нахождения решения называется интегрированием. Интегрируя уравнение с частными производными, находят семейство решений, зависящее от произвольных функций, а не только от произвольных постоянных, как это имеет место в случае обыкновенного дифференциального уравнения. Это семейство решений, зависящее от произвольных функций, называется общим решением уравнения с частными производными.
Уравнение вида
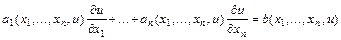 ,
,
где 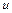 - неизвестная функция от независимых переменных
- неизвестная функция от независимых переменных 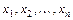 ;
;  ,
, 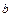 - заданные функции своих аргументов, называется квазилинейным уравнением в частных производных первого порядка. Задачей Коши для этого уравнения называется задача о нахождении среди всех решений этого уравнения такого решения
- заданные функции своих аргументов, называется квазилинейным уравнением в частных производных первого порядка. Задачей Коши для этого уравнения называется задача о нахождении среди всех решений этого уравнения такого решения 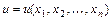 , которое удовлетворяло бы начальному условию
, которое удовлетворяло бы начальному условию 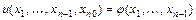 , где
, где 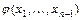 - заданная непрерывно дифференцируемая функция своих аргументов;
- заданная непрерывно дифференцируемая функция своих аргументов; 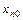 - заданное число.
- заданное число.
В случае уравнения 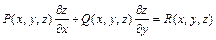 задача Коши состоит в нахождении решения
задача Коши состоит в нахождении решения 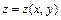 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 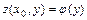 или условию
или условию 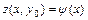 .
.
Интегрирование уравнения 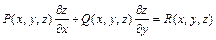 сводится к интегрированию соответствующей ему системы обыкновенных дифференциальных уравнений в симметрической форме:
сводится к интегрированию соответствующей ему системы обыкновенных дифференциальных уравнений в симметрической форме:
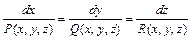 .
.
Если 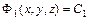 и
и 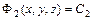 - независимые интегралы этой системы, то равенство
- независимые интегралы этой системы, то равенство 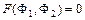 , где
, где 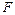 - произвольная непрерывно дифференцируемая функция, является общим решением уравнения в частных производных в неявной форме. Разрешив его относительно
- произвольная непрерывно дифференцируемая функция, является общим решением уравнения в частных производных в неявной форме. Разрешив его относительно 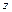 , если
, если 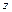 входит только в один из интегралов
входит только в один из интегралов 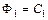 или
или 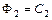 , получим общее решение в явной форме
, получим общее решение в явной форме 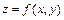 , где
, где 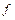 - произвольная непрерывно дифференцируемая функция.
- произвольная непрерывно дифференцируемая функция.
Для нахождения частного решения, подставив начальное условие 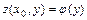 в интегралы
в интегралы 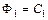 и
и 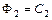 , получим два уравнения вида
, получим два уравнения вида 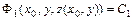 ,
,  . Исключив из них
. Исключив из них 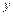 , получим равенство, связывающее
, получим равенство, связывающее 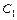 и
и 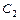 . Подставив в которое вместо
. Подставив в которое вместо 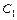 и
и 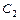 левые части интегралов
левые части интегралов 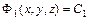 и
и 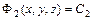 , получим искомое частное решение. Аналогично находится частное решение для начального условия
, получим искомое частное решение. Аналогично находится частное решение для начального условия 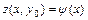 .
.
В задачах 9.321-9.322 найти общие решения простейших дифференциальных уравнений в частных производных.
9.321 а) 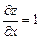 , где
, где 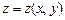 ; б)
; б) 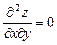 .
.
9.322 а) 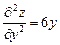 , где
, где 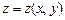 ; б)
; б) 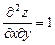 .
.
В задачах 9.323-9.328 найти общие решения уравнений в частных производных первого порядка.
9.323 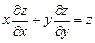 . 9.324
. 9.324 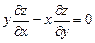 .
.
9.325 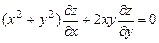 . 9.326
. 9.326 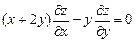 .
.
9.327 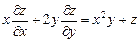 . 9.328
. 9.328 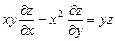 .
.
В задачах 9.329-9.330 найти частные решения уравнений в частных производных первого порядка, удовлетворяющие указанным условиям.
9.329 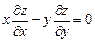 ;
; 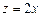 при
при 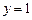 .
.
9.330 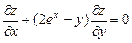 ;
; 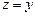 при
при 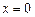 .
.
Уравнение вида
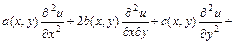
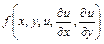 =0,
=0,
где  -неизвестная функция от независимых переменных
-неизвестная функция от независимых переменных 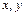 ;
; 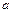 ,
, 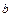 ,
, 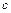 ,
, 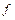 - заданные в области
- заданные в области 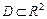 функции своих аргументов, называется квазилинейным дифференциальным уравнением в частных производных второго порядка. Его тип определяется знаком выражения
функции своих аргументов, называется квазилинейным дифференциальным уравнением в частных производных второго порядка. Его тип определяется знаком выражения 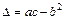 . А именно: 1) если
. А именно: 1) если 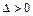 в некоторой точке
в некоторой точке 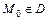 , то уравнение имеет эллиптический тип в этой точке; 2) если
, то уравнение имеет эллиптический тип в этой точке; 2) если 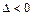 , то уравнение имеет гиперболический тип; 3) если
, то уравнение имеет гиперболический тип; 3) если 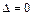 , то уравнение имеет параболический тип. Данное уравнение может менять свой тип при переходе из одной точки области
, то уравнение имеет параболический тип. Данное уравнение может менять свой тип при переходе из одной точки области 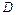 в другую. Например, уравнение
в другую. Например, уравнение 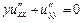 является уравнением эллиптического типа в точках плоскости
является уравнением эллиптического типа в точках плоскости 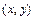 ,
, 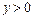 , параболического типа в точках
, параболического типа в точках 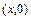 и гиперболического типа в точках
и гиперболического типа в точках 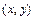 ,
, 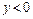 .
.
Уравнение 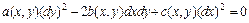 называется характеристическим, а его общие интегралы
называется характеристическим, а его общие интегралы 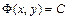 и
и 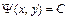 - характеристиками уравнения в частных производных.
- характеристиками уравнения в частных производных.
Характеристики используются для приведения квазилинейного уравнения в частных производных второго порядка к каноническому виду.
Для уравнения гиперболического типа (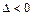 ) характеристики действительны и различны. Подстановкой
) характеристики действительны и различны. Подстановкой 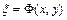 и
и 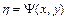 , уравнение приводится к каноническому виду
, уравнение приводится к каноническому виду
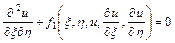 .
.
Для уравнения эллиптического типа (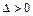 ) характеристики комплексные и комплексно сопряжены (
) характеристики комплексные и комплексно сопряжены (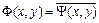 ). Подстановкой
). Подстановкой 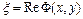 и
и 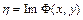 , уравнение приводится к каноническому виду
, уравнение приводится к каноническому виду 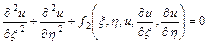 .
.
Для уравнения параболического типа (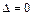 ) имеется только одна характеристика
) имеется только одна характеристика 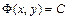 . Подстановкой
. Подстановкой 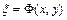 и
и 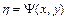 , где
, где 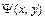 - произвольная функция, независимая с
- произвольная функция, независимая с 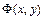
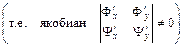 уравнение приводится к каноническому виду
уравнение приводится к каноническому виду 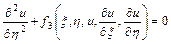 .
.
В задачах 9.331-9.339 определить тип дифференциальных уравнений в частных производных второго порядка и привести их к каноническому виду.
9.331 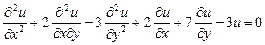 .
.
9.332 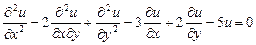 .
.
9.333 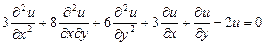 .
.
9.334 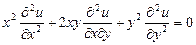 .
.
9.335 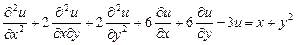 .
.
9.336  .
.
9.337 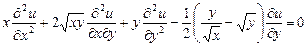 .
.
9.338 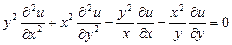 .
.
9.339 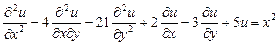 .
.
В задачах 9.340-9.345, используя формулу Даламбера
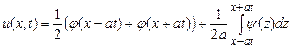 , найти
, найти
решение задачи Коши для волнового уравнения на прямой:
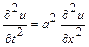
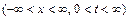 ;
; 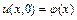 ;
; 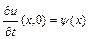
9.340 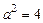 ,
, 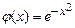 ,
, 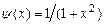 .
.
9.341 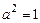 ,
, 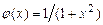 ,
, 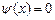 .
.
9.342 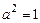 ,
, 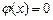 ,
, 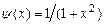 .
.
9.343 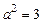 ,
, 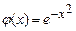 ,
, 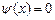 .
.
9.344 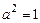 ,
, 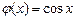 ,
, 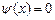 .
.
9.345 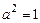 ,
, 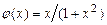 ,
, 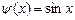 .
.
Задачей Штурма-Лиувилля называется задача о нахождении отличных от нуля решений (собственных функций) 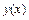 ,
, 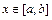 , дифференциального уравнения
, дифференциального уравнения 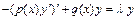 , удовлетворяющих граничным условиям вида
, удовлетворяющих граничным условиям вида 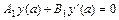 ,
, 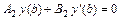 , где
, где 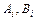 - заданные числа, а также о нахождении значений параметра
- заданные числа, а также о нахождении значений параметра 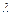 (собственных значений), при которых существуют такие решения.
(собственных значений), при которых существуют такие решения.
В задачах 9.346-9.348 найти собственные числа и собственные функции следующих задач Штурма-Лиувилля.
9.346 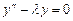 ,
, 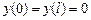 .
.
9.347 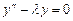 ,
, 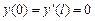 .
.
9.348 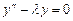 ,
, 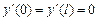 .
.
Метод Фурье является одним из наиболее распространённых аналитических методов решения уравнений математической физики и состоит в следующем. Искомая функция 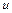 , зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. Например, если
, зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. Например, если 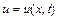 , то функция
, то функция 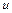 ищется в виде
ищется в виде 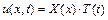 ; если
; если 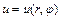 , то - в виде
, то - в виде 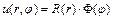 . После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, часть из которых вместе с краевыми условиями исходной задачи являются краевыми задачами Штурма-Лиувилля. Искомое решение представляется рядом по произведениям собственных функций этих задач Штурма-Лиувилля.
. После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, часть из которых вместе с краевыми условиями исходной задачи являются краевыми задачами Штурма-Лиувилля. Искомое решение представляется рядом по произведениям собственных функций этих задач Штурма-Лиувилля.
В задачах 9.349-9.352 найти решение смешанной краевой задачи для волнового уравнения на отрезке методом Фурье.
9.349 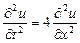 ,
, 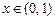 ,
, 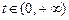 ;
;
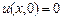 ,
, 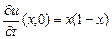 ,
,  .
.
9.350 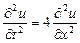 ,
, 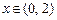 ,
, 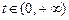 ;
;
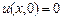 ,
, 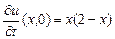 ,
, 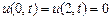 .
.
9.351 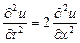 ,
, 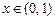 ,
, 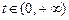 ;
;
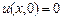 ,
, 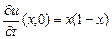 ,
,  .
.
9.352 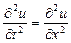 ,
, 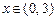 ,
, 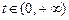 ;
;
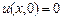 ,
, 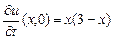 ,
,  .
.
В задачах 9.353-9.356 найти решение методом Фурье смешанной краевой задачи для уравнения теплопроводности на отрезке.
9.353 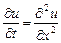 ,
, 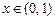 ,
, 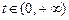 ;
;
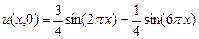 ,
,  .
.
9.354 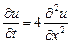 ,
, 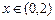 ,
, 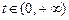 ;
;
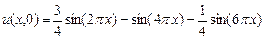 ,
, 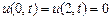 .
.
9.355 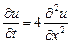 ,
, 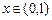 ,
, 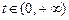 ;
;
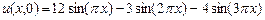 ,
,  .
.
9.356 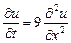 ,
, 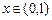 ,
, 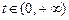 ;
;
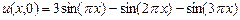 ,
,  .
.
В задачах 9.357-9.360 найти решение методом Фурье краевой задачи Дирихле для уравнения Лапласа в круге.
9.357 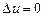 ,
, 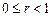 ,
, 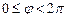 ,
, 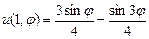
9.358 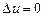 ,
, 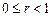 ,
, 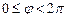 ,
,
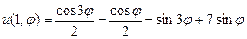 .
.
9.359 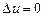 ,
, 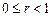 ,
, 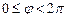 ,
,
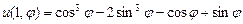
9.360 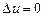 ,
, 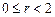 ,
, 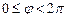 ,
,
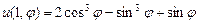 .
.
 2015-03-20
2015-03-20 6301
6301
