Если функция 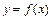 интегрируема на отрезке
интегрируема на отрезке 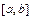 , то несобственным интегралом первого рода от функции
, то несобственным интегралом первого рода от функции 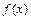 на промежутке
на промежутке 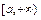 называется
называется 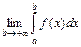 и обозначается
и обозначается 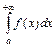 , т.е.
, т.е. 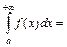
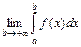 . Аналогично:
. Аналогично: 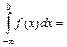
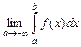 .
.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Несобственный интеграл 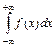 определяется равенством:
определяется равенством:
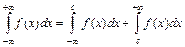 , где
, где 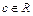 - произвольное число, причём интеграл в левой части равенства сходится, если сходятся оба интеграла в правой части.
- произвольное число, причём интеграл в левой части равенства сходится, если сходятся оба интеграла в правой части.
Признаки сходимости и расходимости.
1. Пусть при 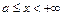
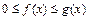 . Тогда, если
. Тогда, если 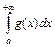 сходится, то сходится и
сходится, то сходится и 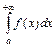 , если
, если 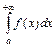 расходится, то расходится и
расходится, то расходится и 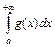 .
.
2. Если 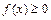 и
и 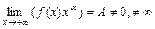 , т.е.
, т.е. 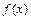 ~
~ 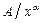 при
при 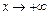 , то: 1) при
, то: 1) при 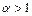
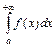 сходится; 2) при
сходится; 2) при 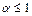 расходится.
расходится.
Аналогично устанавливаются признаки сходимости и расходимости интеграла 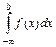 .
.
В задачах 7.205-7.213 вычислить несобственные интегралы (или установить их расходимость).
7.205 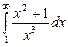 . 7.206
. 7.206 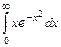 . 7.207
. 7.207 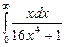 .
.
7.208 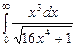 . 7.209
. 7.209 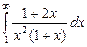 . 7.210
. 7.210 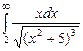 .
.
7.211 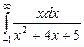 . 7.212
. 7.212 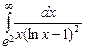 . 7.213
. 7.213 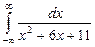 .
.
В задачах 7.214-7.219, используя признаки сходимости, исследовать сходимость следующих интегралов:
7.214 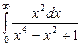 . 7.215
. 7.215 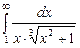 . 7.216
. 7.216 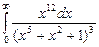 .
.
7.217 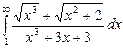 7.218
7.218 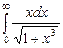 7.219
7.219 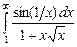 .
.
 2015-03-20
2015-03-20 330
330








