Вычисление интегралов вида 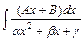 и
и 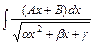 , выделяя в квадратном трёхчлене
, выделяя в квадратном трёхчлене 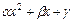 полный квадрат
полный квадрат 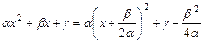 и делая замену переменной интегрирования
и делая замену переменной интегрирования 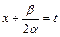 , сводят к вычислению табличных интегралов (см. приложение 4) и интегралов вида
, сводят к вычислению табличных интегралов (см. приложение 4) и интегралов вида 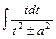 и
и 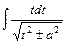 , которые сводят к табличным заменой переменной
, которые сводят к табличным заменой переменной 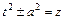 .
.
Вычисление интегралов вида 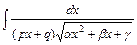 , делая замену переменной интегрирования
, делая замену переменной интегрирования 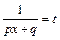 , сводят к вычислению интегралов, рассмотренных выше.
, сводят к вычислению интегралов, рассмотренных выше.
В задачах 7.70-7.80 найти следующие интегралы от функций, содержащих квадратный трёхчлен:
7.70 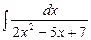 . 7.71
. 7.71 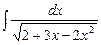 . 7.72
. 7.72 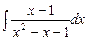 .
.
7.73 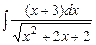 . 7.74
. 7.74 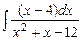 . 7.75
. 7.75 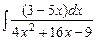 .
.
7.76 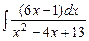 . 7.77
. 7.77 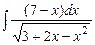 . 7.78
. 7.78 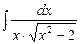 .
.
7.79 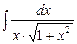 . 7.80
. 7.80 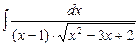 .
.
Рациональной дробью называется рациональная функция 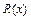 вида
вида 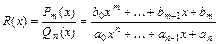 . Если
. Если 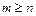 , то дробь не правильная, в противном случае – правильная. Всякую неправильную дробь всегда можно представить в виде
, то дробь не правильная, в противном случае – правильная. Всякую неправильную дробь всегда можно представить в виде 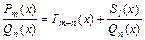 , где
, где 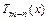 ,
, 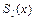 -многочлены от
-многочлены от 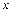 , причём
, причём 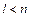 . Выделение целой части (многочлена
. Выделение целой части (многочлена 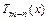 ) в неправильной дроби производят делением числителя на знаменатель, выполняемое «уголком». Таким образом, интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
) в неправильной дроби производят делением числителя на знаменатель, выполняемое «уголком». Таким образом, интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
Интегрирование правильной рациональной дроби основано на её представлении в виде конечной суммы простейших дробей вида 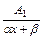 ,
, 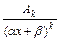
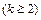 ,
, 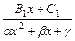 ,
, 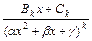
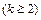 , причём трёхчлен
, причём трёхчлен 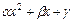 не имеет действительных корней. Вид этого разложения определяется разложением знаменателя
не имеет действительных корней. Вид этого разложения определяется разложением знаменателя 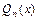 дроби на линейные и квадратичные множители (не имеющие действительных корней).
дроби на линейные и квадратичные множители (не имеющие действительных корней).
Каждому линейному множителю вида 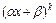 , где
, где 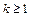 , в разложении соответствует сумма из
, в разложении соответствует сумма из 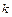 простейших дробей вида
простейших дробей вида 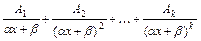 . Каждому квадратичному множителю вида
. Каждому квадратичному множителю вида 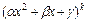 , где
, где 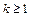 , в разложении соответствует сумма из
, в разложении соответствует сумма из 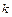 простейших дробей вида
простейших дробей вида 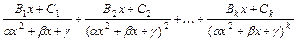 .
.
Неизвестные постоянные 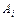 ,
, 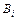 ,
, 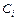 в разложении правильной рациональной дроби
в разложении правильной рациональной дроби 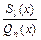 в сумму простейших дробей определяют методом неопределённых коэффициентов. Для этого правую часть искомого разложения приводят к общему знаменателю (им будет многочлен
в сумму простейших дробей определяют методом неопределённых коэффициентов. Для этого правую часть искомого разложения приводят к общему знаменателю (им будет многочлен 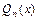 ), после чего у получившегося в числителе многочлена с неизвестными постоянными и у многочлена
), после чего у получившегося в числителе многочлена с неизвестными постоянными и у многочлена 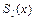 приравнивают коэффициенты при одинаковых степенях
приравнивают коэффициенты при одинаковых степенях 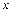 . В результате получают систему линейных уравнений, решая которую находят неизвестные постоянные. Можно также определять
. В результате получают систему линейных уравнений, решая которую находят неизвестные постоянные. Можно также определять 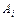 ,
, 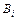 ,
, 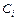 , подставляя в равенство, полученное приравниванием числителя
, подставляя в равенство, полученное приравниванием числителя 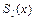 к числителю дроби с неизвестными постоянными, полученной после приведения простейших дробей к общему знаменателю
к числителю дроби с неизвестными постоянными, полученной после приведения простейших дробей к общему знаменателю 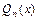 , вместо
, вместо 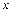 некоторые специально подобранные числа (обычно действительные корни знаменателя
некоторые специально подобранные числа (обычно действительные корни знаменателя 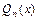 ) (метод частных значений). Часто, при нахождении неизвестных постоянных, комбинируют оба способа.
) (метод частных значений). Часто, при нахождении неизвестных постоянных, комбинируют оба способа.
Интегрирование простейшей дроби 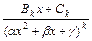
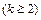 , выделением полного квадрата
, выделением полного квадрата 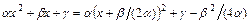 и заменой
и заменой 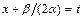 , сводят к вычислению интеграла вида
, сводят к вычислению интеграла вида 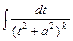 . Для вычисления такого интеграла используют подстановку
. Для вычисления такого интеграла используют подстановку 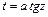 .
.
В задачах 7.81-7.90 найти следующие интегралы от рациональных функций:
7.81 а) 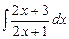 ; б)
; б) 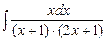 ; в)
; в) 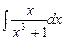 .
.
7.82 а) 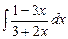 ; б)
; б) 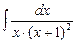 ; в)
; в) 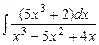 .
.
7.83 а) 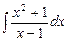 ; б)
; б) 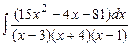 ; в)
; в) 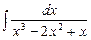 .
.
7.84 а) 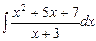 ; б)
; б) 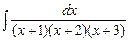 ; в)
; в) 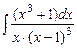 .
.
7.85 а) 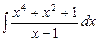 ; б)
; б) 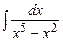 ; в)
; в) 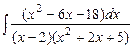 .
.
7.86 а) 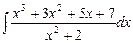 ; б)
; б) 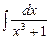 ; в)
; в) 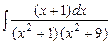 .
.
7.87 а) 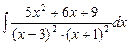 ; б)
; б) 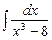 ; в)
; в) 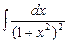 .
.
7.88 а) 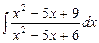 ; б)
; б) 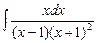 ; в)
; в) 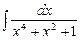 .
.
7.89 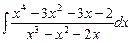 ; 7.90
; 7.90 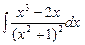 .
.
Интегралы вида 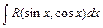 , где
, где 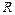 -рациональная функция относительно аргументов
-рациональная функция относительно аргументов 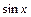 и
и 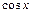 , приводятся к интегралам вида
, приводятся к интегралам вида 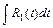 , где
, где 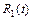 -рациональная функция относительно аргумента
-рациональная функция относительно аргумента 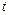 , с помощью универсальной тригонометрической подстановки
, с помощью универсальной тригонометрической подстановки 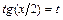 . При этом используются формулы:
. При этом используются формулы: 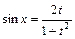 ,
, 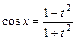 ,
, 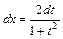 .
.
Применение универсальной подстановки, иногда приводит к громоздким вычислениям. В частных случаях используют подстановки:
1) 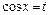 , если
, если 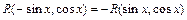 , при этом:
, при этом: 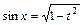 ,
, 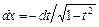 ;
;
2) 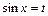 , если
, если 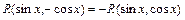 , при этом:
, при этом: 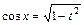 ,
, 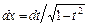 ;
;
3) 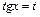 , если
, если 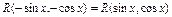 или
или 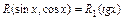 , при этом:
, при этом: 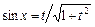 ,
, 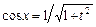 ,
, 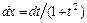 ;
;
4) 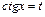 , если
, если 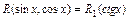 , при этом
, при этом 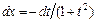 . Здесь
. Здесь 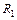 - рациональная функция относительно аргументов
- рациональная функция относительно аргументов 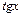 ,
, 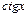 .
.
Интегралы вида 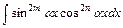 , где
, где 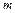 ,
, 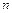 - целые неотрицательные числа, вычисляют, преобразуя подынтегральную функцию с помощью формул:
- целые неотрицательные числа, вычисляют, преобразуя подынтегральную функцию с помощью формул: 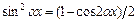 ,
, 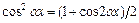 .
.
Интегралы вида 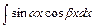 ,
, 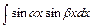
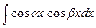 , вычисляют, преобразуя подынтегральную функцию по формулам:
, вычисляют, преобразуя подынтегральную функцию по формулам:
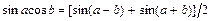 ;
;
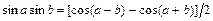 ;
;
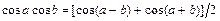 .
.
В задачах 7.91-7.118 найти следующие интегралы от тригонометрических функций:
7.91 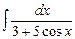 . 7.92
. 7.92 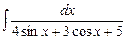 . 7.93
. 7.93 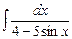 .
.
7.94 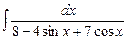 . 7.95
. 7.95 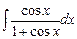 . 7.96
. 7.96 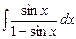 .
.
7.97 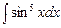 . 7.98
. 7.98 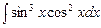 . 7.99
. 7.99 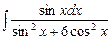 .
.
7.100 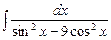 . 7.101
. 7.101 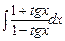 . 7.102
. 7.102 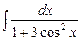 .
.
7.103 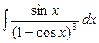 . 7.104
. 7.104 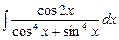 .
.
7.105 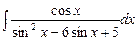 . 7.106
. 7.106 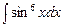 . 7.107
. 7.107 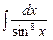 .
.
7.108 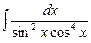 . 7.109
. 7.109 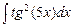 . 7.110
. 7.110 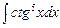 .
.
7.111 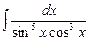 . 7.112
. 7.112 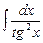 . 7.113
. 7.113 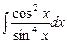 .
.
7.114 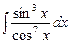 . 7.115
. 7.115 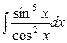 . 7.116
. 7.116 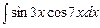 .
.
7.117 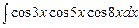 . 7.118
. 7.118 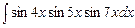 .
.
Интегрирование гиперболических функций аналогично интегрированию тригонометрических функций. При этом используются формулы:
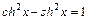 ;
; 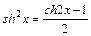 ;
; 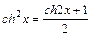 ;
; 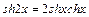 .
.
В задачах 7.119-7.130 найти следующие интегралы от гиперболических функций:
7.119 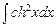 . 7.120
. 7.120 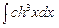 . 7.121
. 7.121 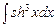 . 7.122
. 7.122 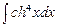 . 7.123
. 7.123 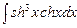 . 7.124
. 7.124 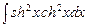 .
.
7.125 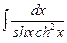 . 7.126
. 7.126 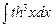 . 7.127
. 7.127 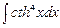 .
.
7.128 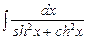 . 7.129
. 7.129 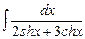 . 7.130
. 7.130 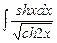 .
.
Интегралы вида 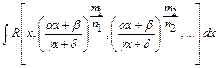 , где
, где 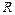 -рациональная функция своих аргументов,
-рациональная функция своих аргументов, 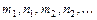 -целые числа, вычисляются с помощью подстановки
-целые числа, вычисляются с помощью подстановки 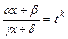 , где
, где 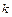 - наименьший общий знаменатель дробей
- наименьший общий знаменатель дробей 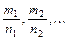 .
.
Вычисление интегралов вида 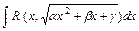 , где
, где 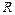 -рациональная функция своих аргументов, выделением полного квадрата в квадратном трёхчлене
-рациональная функция своих аргументов, выделением полного квадрата в квадратном трёхчлене 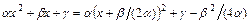 и заменой
и заменой 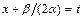 , сводится к вычислению интегралов вида:
, сводится к вычислению интегралов вида:
1) 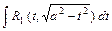 ; 2)
; 2) 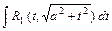 ; 3)
; 3) 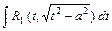 , где
, где 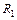 - рациональная функция своих аргументов.
- рациональная функция своих аргументов.
Последние интегралы, соответственно, с помощью тригонометрических или гиперболических подстановок:
1) 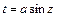 или
или 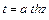 ;
;
2) 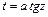 или
или 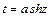 ;
;
3) 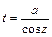 или
или 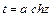
приводятся к интегралам вида 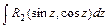 или
или 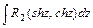 , где
, где 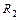 - рациональная функция своих аргументов
- рациональная функция своих аргументов
В задачах 7.131-7.140 найти следующие интегралы от иррациональных функций:
7.131 а) 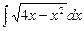 ; б)
; б) 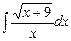 ; в)
; в) 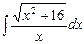 .
.
7.132 а) 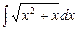 ; б)
; б) 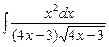 ; в)
; в) 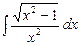 .
.
7.133 а) 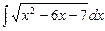 ; б)
; б) 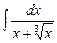 ; в)
; в) 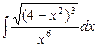 .
.
7.134а) 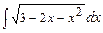 ; б)
; б) 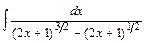 ; в)
; в) 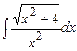
7.135 а) 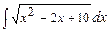 ; б)
; б) 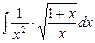 ; в)
; в) 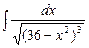 .
.
7.136 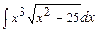 . 7.137
. 7.137 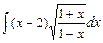 . 7.138
. 7.138 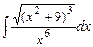
7.139 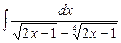 . 7.140
. 7.140 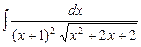 .
.
 2015-03-20
2015-03-20 444
444








