Частной производной (1-ого порядка) функции 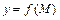 в точке
в точке 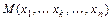 по переменной
по переменной 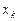 называется предел
называется предел 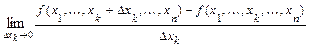 , если этот предел существует. Частную производную обозначают
, если этот предел существует. Частную производную обозначают 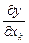 или
или 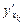 .
.
Частные производные вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что все аргументы функции, кроме аргумента 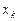 , по которому берётся производная, постоянны.
, по которому берётся производная, постоянны.
Частными производными второго порядка функции 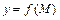 называются частные производные от её частных производных первого порядка. При этом используются обозначения:
называются частные производные от её частных производных первого порядка. При этом используются обозначения:
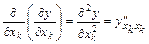 ,
, 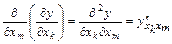 (
(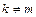 ).
).
Производные 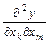 (
(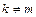 ) называются смешанными. Аналогично определяются и обозначаются частные производные порядка выше второго. Для функции
) называются смешанными. Аналогично определяются и обозначаются частные производные порядка выше второго. Для функции 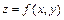 частные производные обозначаются:
частные производные обозначаются:
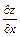 ,
, 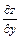 ,
, 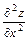 ,
, 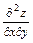 ,
, 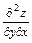 ,
, 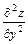 ,… или
,… или 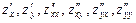 ,….
,….
Если смешанные частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования.
В задачах 6.22-6.32 найти частные производные 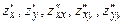 от следующих функций:
от следующих функций:
6.22 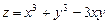 . 6.23
. 6.23 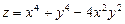 .
.
6.24 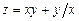 . 6.25
. 6.25 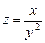 . 6.26
. 6.26 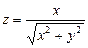 . 6.27
. 6.27 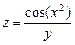 . 6.28
. 6.28 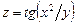 . 6.29
. 6.29 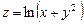 . 6.30
. 6.30 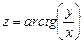 . 6.31
. 6.31 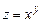 . 6.32
. 6.32 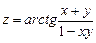 .
.
В задачах 6.33-6.34 найти частные производные 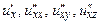 от следующих функций:
от следующих функций:
6.33 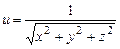 . 6.34
. 6.34 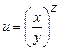 .
.
6.35 Проверить равенство 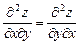 , если
, если
а) 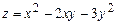 ; б)
; б) 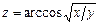 .
.
6.36 Проверить равенство 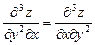 , если
, если 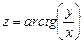
В задачах 6.37-6.40 найти указанные частные производные:
6.37 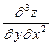 , если
, если 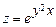 . 6.38
. 6.38 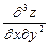 , если
, если 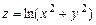 . 6.39
. 6.39 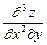 ,если
,если 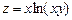 . 6.40
. 6.40 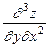 ,если
,если 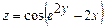 .
.
 2015-03-20
2015-03-20 466
466







