Если функция 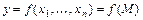 дифференцируема
дифференцируема 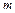 раз в точке
раз в точке 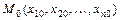 , то при
, то при 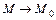 имеет место формула Тейлора (порядка
имеет место формула Тейлора (порядка 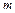 ) с остаточным членом в форме Пеано
) с остаточным членом в форме Пеано
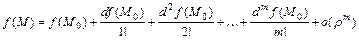 ,
,
где 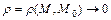 при
при 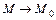 . Частный случай формулы Тейлора в точке
. Частный случай формулы Тейлора в точке 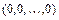 называется формулой Маклорена.
называется формулой Маклорена.
6.79 Разложить по формуле Тейлора следующие функции в окрестности указанных точек:
а) 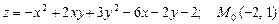 ;
;
б) 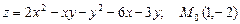 ;
;
в) 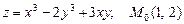 ;
;
г) 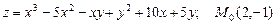 ;
;
д) 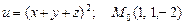 ;
;
е) 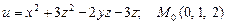 .
.
6.80 Выписать члены до второго порядка включительно формулы Тейлора для функции 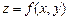 в окрестности точки
в окрестности точки 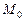 :
:
а) 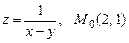 ; б)
; б) 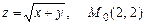 ;
;
в) 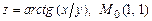 .
.
6.81 Разложить функции 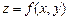 по формуле Маклорена до членов третьего порядка включительно:
по формуле Маклорена до членов третьего порядка включительно:
а) 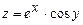 ; б)
; б) 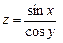 .
.
 2015-03-20
2015-03-20 307
307








