Полным приращением функции 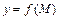 в точке
в точке 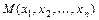 , соответствующим приращениям аргументов
, соответствующим приращениям аргументов 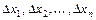 называется разность
называется разность 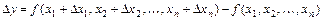 .
.
Функция 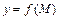 называется дифференцируемой в точке
называется дифференцируемой в точке 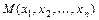 , если её полное приращение может быть представлено в виде
, если её полное приращение может быть представлено в виде 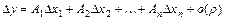 , где
, где 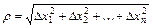
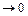 при
при 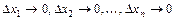 ,
, 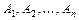 - числа, не зависящие от
- числа, не зависящие от 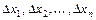 .
.
Полным дифференциалом 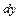 функции
функции 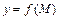 в точке
в точке 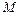 называется главная, линейная относительно
называется главная, линейная относительно 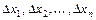 часть
часть 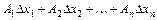 полного приращения
полного приращения 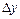 функции, равная
функции, равная 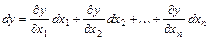 , где
, где 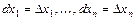 .
.
Функция 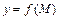 , обладающая в точке
, обладающая в точке 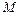 непрерывными частными производными, всегда имеет в этой точке полный дифференциал
непрерывными частными производными, всегда имеет в этой точке полный дифференциал 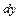 . Для функции
. Для функции 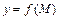 дифференцируемость в точке равносильна существованию в этой точке её полного дифференциала.
дифференцируемость в точке равносильна существованию в этой точке её полного дифференциала.
Форма записи первого дифференциала не изменится и в том случае, если переменные 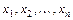 являются функциями новых, независимых переменных (свойство инвариантности формы первого дифференциала).
являются функциями новых, независимых переменных (свойство инвариантности формы первого дифференциала).
Дифференциалом 2-ого порядка функции 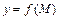 называется дифференциал от её первого дифференциала и обозначается
называется дифференциал от её первого дифференциала и обозначается 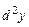 , т. е.
, т. е. 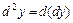 . В общем дифференциалом порядка
. В общем дифференциалом порядка 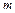 называется дифференциал от дифференциала
называется дифференциал от дифференциала 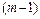 -ого порядка и обозначается
-ого порядка и обозначается 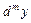 , т.е.
, т.е. 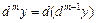 .
.
Если 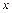 - независимая переменная, то для нахождения дифференциала
- независимая переменная, то для нахождения дифференциала 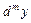 функции
функции 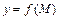 справедлива символическая формула
справедлива символическая формула 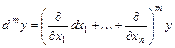 , формально раскрываемая по биномиальному закону. Например, для функции
, формально раскрываемая по биномиальному закону. Например, для функции 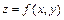 справедливы формулы:
справедливы формулы: 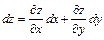 ,
, 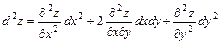 ,
,
а для функции 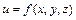 - формулы:
- формулы: 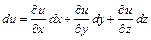 ,
,
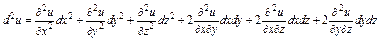 .
.
Для функции 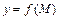
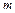 -кратная дифференцируемость в точке
-кратная дифференцируемость в точке 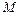 равносильна существованию в этой точке её полного дифференциала
равносильна существованию в этой точке её полного дифференциала 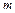 -ого порядка
-ого порядка 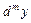 .
.
Если функция 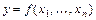
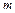 раз дифференцируема в точке
раз дифференцируема в точке 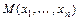 , то в этой точке значение любой смешанной частной производной
, то в этой точке значение любой смешанной частной производной 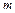 -ого порядка не зависит от порядка дифференцирования.
-ого порядка не зависит от порядка дифференцирования.
В задачах 6.41-6.46 найти дифференциалы первого и второго порядков от следующих функций:
6.41 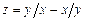 . 6.42
. 6.42 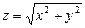 . 6.43
. 6.43 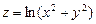 .
.
6.44 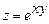 . 6.45
. 6.45 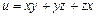 . 6.46
. 6.46 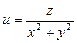 .
.
6.47 Найти значение полного дифференциала функции 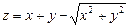 при
при 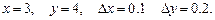
6.48 Найти значение полного дифференциала функции 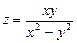 при
при 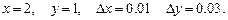
Первый дифференциал применяют для приближённого вычисления значений функции 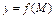 в малой окрестности точки
в малой окрестности точки 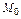 , в которой функция дифференцируема, по формуле:
, в которой функция дифференцируема, по формуле: 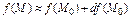 .
.
В частности, для функции 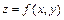 по формуле:
по формуле: 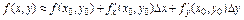 , где
, где 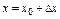 ,
, 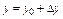 . Чем меньше значение
. Чем меньше значение 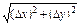 , тем точнее формула.
, тем точнее формула.
6.49 Вычислить приближенно:
а) 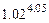 ; б)
; б) 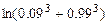 ; в)
; в) 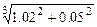 ; г)
; г) 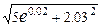 ; д)
; д) 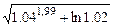 ; е)
; е) 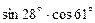 ;
;
ж) 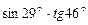 ; з)
; з) 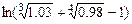 .
.
6.50 На сколько приближённо изменятся диагональ и площадь прямоугольника со сторонами 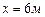 ,
, 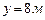 , если первая сторона увеличится на
, если первая сторона увеличится на 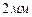 , а вторая уменьшится на
, а вторая уменьшится на 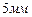 ?
?
6.51 Центральный угол сектора 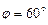 увеличился на
увеличился на 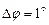 . На сколько следует приближённо уменьшить радиус сектора
. На сколько следует приближённо уменьшить радиус сектора 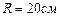 , чтобы площадь сектора осталась без изменения?
, чтобы площадь сектора осталась без изменения?
6.52 Прямоугольный параллелепипед имеет измерения: 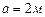 ,
, 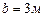 ,
, 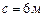 . На сколько приближённо изменится длина его диагонали, если
. На сколько приближённо изменится длина его диагонали, если 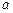 увеличится на
увеличится на 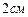 ,
, 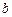 увеличится на
увеличится на 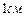 ,
, 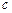 уменьшится на
уменьшится на 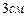 .
.
6.53 Цилиндрический стакан имеет внутренние размеры: радиус основания R =2.5 м, высоту Н =4м и толщину стенок l =1дм. Найти приближенно объем материала, затраченного на изготовление стакана.
6.54 В усеченном конусе радиусы оснований R =20 см, r =10 см и высота h =30 см. Как приближенно изменится объем конуса 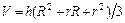 , если R увеличить на 2 мм, r увеличить на 3 мм, а h уменьшить на 1 мм?
, если R увеличить на 2 мм, r увеличить на 3 мм, а h уменьшить на 1 мм?
6.55 Найти в указанной точке второй дифференциал функций:
а) 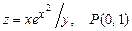 ; б)
; б) 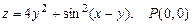 .
.
 2015-03-20
2015-03-20 1311
1311
