2015-01-21
1296
Пусть в области T трехмерного пространства задано векторное поле: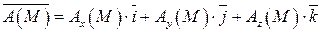 
.
Основными операциями данногополя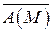 
являются дивергенция 
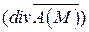и ротор 
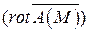. В декартовых координатах:
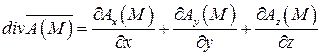, (33)
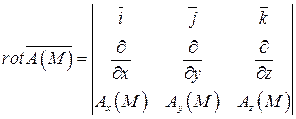(34)
Потоком векторного поля 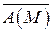через выбранную сторону поверхности S называется поверхностный интеграл 1-го рода по поверхности S от функции:
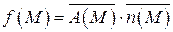
где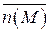 
- орт нормали к выбранной стороне поверхности S:
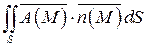(35)
ТеоремаГаусса-Остроградского (о вычислении потока векторного поля).
Пусть в некоторой замкнутой пространственной области T, ограниченной поверхностью S, задано векторное поле 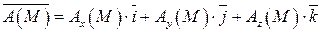, где функции Ax (M), Ay (M), Az (M) имеют непрерывные частные производные. Тогда имеет место формула:
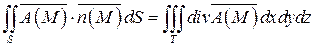(36)
Интегралом типа работы векторного поля
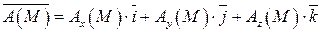
по линии L называется криволинейный интеграл 2-го рода вида:
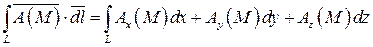(37)
Теорема Стокса (о вычислении циркуляции векторного поля).
Пусть на поверхности S и ее границе L задано векторное поле
,
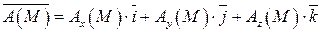где функции Ax (M), Ay (M), Az (M) имеют непрерывные частные производные. Тогда имеет место формула:
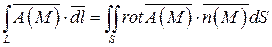, (38)
где 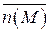- орт нормали к поверхности S, направленный так, что при обходе контура L область, ограниченная L, остается слева, если смотреть с конца орта нормали.
Задание 1. Дано векторное поле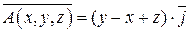 
и плоскость P:
2 x-y+ 2 z- 2=0, которая с координатными плоскостями образует пирамиду T. Пусть поверхность SABC – грань пирамиды(треугольник АВС), принадлежащая плоскости P, LABC - контур, ограничивающий SABC.
Вычислить:
1) поток векторного поля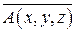 
через полную поверхность S пирамиды T в направлении внешней нормали (непосредственно и по теореме Гаусса-Остроградского);
2)циркуляцию данного векторного поля 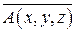по контуру LABC (непосредственно и по теореме Стокса).
Решение.
1) Изобразим пирамиду (рис.13).
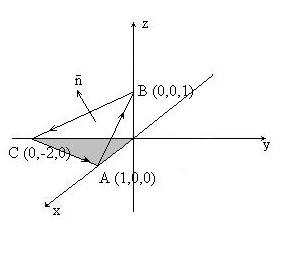
Рис. 13
Тогда поток данного векторного поля равен:
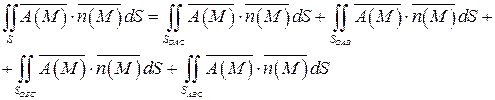
Вычислим каждый из интегралов правой части последнего равенства.
а)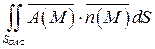 
Уравнение поверхности SOAC: z= 0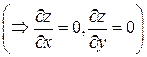 
; орт нормали к SOAC имеет вид: 
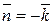; поверхность SOAC проектируется в область DOAC плоскости Oxy (рис. 14).
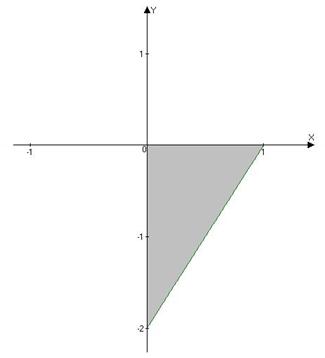
Рис. 14
Так как орт нормали к поверхности 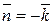, то подынтегральная функция рассматриваемого интеграла 
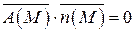. Следовательно,
.
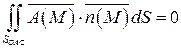б)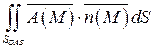 
Уравнение поверхности SOAB: y =0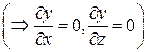 
; орт нормали к SOAB имеет вид: 
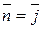; поверхность SOAB проектируется в область DOAB плоскости Oxz (рис.15). Следовательно, в силу формулы (32):
.
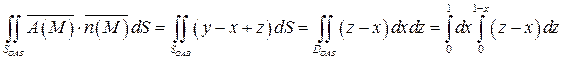Вычислив полученный повторный интеграл, имеем:
.
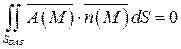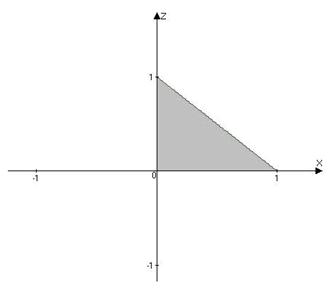
Рис. 15.
в)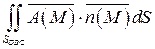 
Уравнение поверхности SOBC: x =0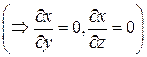 
; орт нормали к SOBC имеет вид: 
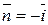; поверхность SOBC проектируется в область DOBC плоскости Oyz (рис.16). Так как орт нормали 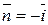, то подынтегральная функция рассматриваемого интеграла 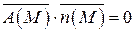. Следовательно,
.
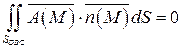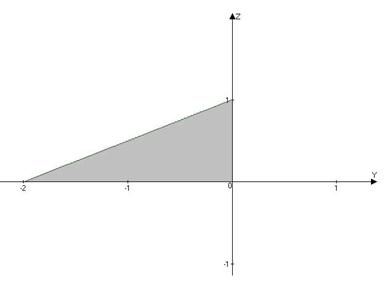
Рис. 16
г)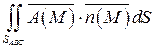 
Уравнение поверхности SABC: 2 x - y +2 z -2=0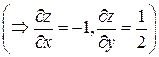 
; орт нормали к SABC имеет вид: 
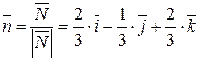; поверхность SABC проектируется в область DABC плоскости Oxy, совпадающую с областью DOAC (рис.14). Следовательно, в силу формулы (32) имеем:
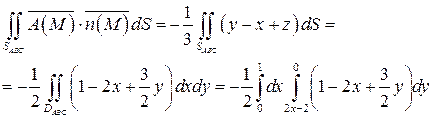
Вычислим полученный повторный интеграл:
.
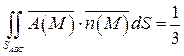Таким образом, поток векторного поля 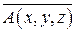через полную поверхность S данной пирамиды T равен:
.
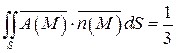2) Вычислим теперь поток данного векторного поля 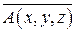через полную поверхность S пирамиды T по теореме Гаусса-Остроградского:
.
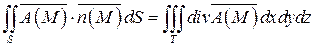Дивергенция данного векторного поля 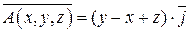равна:
.
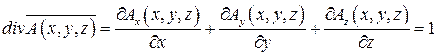Следовательно,
.
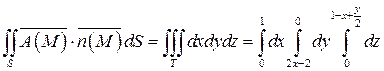Вычисляем полученный тройной интеграл:
.
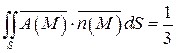Решение 2
1) Вычислим циркуляцию данного векторного поля 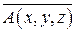по контуру LABC:
.
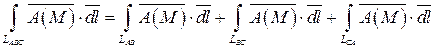Вычислим каждый из интегралов правой части полученного равенства:
а)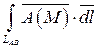 
.
Составим параметрические уравнения отрезка AB:
,
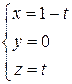где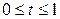 
. Тогда в силу формулы (29) имеем:
.
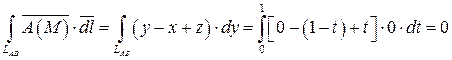б)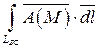 
.
Составим параметрические уравнения отрезка BC:
,
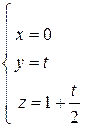где t меняется от 0 до -2. Тогда в силу формулы (29) имеем:
.
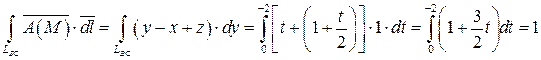в)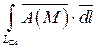 
.
Составим параметрические уравнения отрезка CA:
,
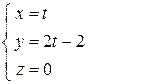где 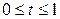. Тогда в силу формулы (29) имеем:
.
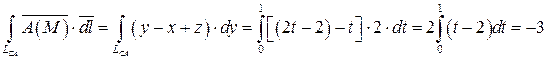Следовательно, циркуляция данного векторного поля 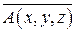по контуру LABC равна: 
.
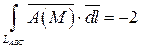2) Вычислим теперь циркуляцию векторного поля 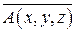по контуру LABC с помощью теоремы Стокса:
.
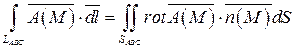Для этого найдем ротор данного векторного поля :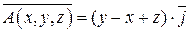
.
Орт нормали к поверхности SABC мы находили при вычислении потока векторного поля :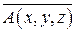 
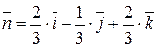(п.1а). Следовательно,
.
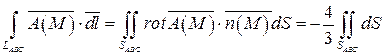Уравнение поверхности SABC: 2 x-y+ 2 z- 2=0 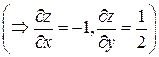; поверхность SABC проектируется в область DABC плоскости Oxy (рис.14). Таким образом, в силу формулы (32) имеем:
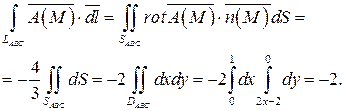
Ряды
