Некоторые физические величины описываются одним лишь числом – это скалярные величины (масса, температура, объем, энергия); для описания других требуется задать величину и направление – это векторы (скорость, сила). Векторы будем обозначать подчеркнутыми буквами (например 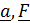 ); та же буква без черты будет обозначать модуль (длину):
); та же буква без черты будет обозначать модуль (длину): 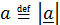 .
.
Сразу же заметим, что векторы в виде направленных отрезков идеально подходят для описания перемещения (трансляции) тела в пространстве, а даже такое простейшее движение тела как вращение вокруг неподвижной оси удобно изобразить в виде кругового вектора 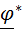 , полностью описывающего и направление вращения и своей длиной угол поворота.
, полностью описывающего и направление вращения и своей длиной угол поворота.
Круговому вектору 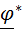 поставим в соответствие прямой вектор
поставим в соответствие прямой вектор 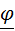 , который перпендикулярен плоскости кругового, а направление согласовано с выбором ориентации пространства:
, который перпендикулярен плоскости кругового, а направление согласовано с выбором ориентации пространства:
 |
 |
 |
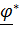 |
| Рис. 1.2. Ориентация пространства |
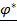 |
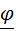 направление кругового видно противчасовой стрелки и левоориентированным, если по часовой стрелке (рис. 1.2).
направление кругового видно противчасовой стрелки и левоориентированным, если по часовой стрелке (рис. 1.2). Векторы и тензоры называются полярными, если при изменении ориентации они не изменяются, и аксиальными, если изменяют знак на противоположный. Из изложенного ясно, что величины, прямо либо косвенно связанные с перемещениями, являются (скорее всего) полярными, а с вращениями – аксиальными, но это необходимо проверять.
На множестве векторов (в векторном пространстве) вводятся операции с векторами, позволяющие не постулировать (как это принято в математике), а доказать привычные правила коммутативности (перестановочности) операций сложения и умножения, (за исключением операции векторного умножения, для которого 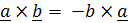 ), дистрибутивности (распределительный закон умножения), ассоциативности (сочетательный закон) сложения.
), дистрибутивности (распределительный закон умножения), ассоциативности (сочетательный закон) сложения.
| Рис. 1.3. Сложение и умножение на число |
| a) |
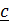 |
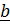 |
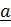 |
| b) |
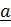 |
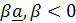 |
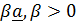 |
1. Сложение векторов:
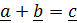 (рис 1.3,а).
(рис 1.3,а). 2.Умножение на число: 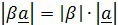 (рис 1.3,b).
(рис 1.3,b).
 . (1.2)
. (1.2)
Независимо от выбора базиса модуль вектора вычисляется по формуле
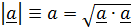 .
.
С помощью скалярного произведения вычисляется проекция вектора 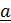 на направление вектора
на направление вектора 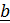 :
: 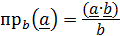 и угол между ними:
и угол между ними:  .
.
В наиболее часто применяемом ортонормированном базисе 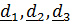 , в котором
, в котором 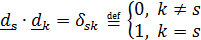 – символ Кронекера,
– символ Кронекера,
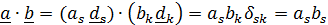 .
.
Здесь применяется правило суммирования по повторяющимся индексам:
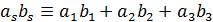 .
.
4. Векторное произведение: 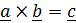 . Векторное произведение непосредственно связано с ориентацией пространства.
. Векторное произведение непосредственно связано с ориентацией пространства.
В результате произведения 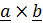 получается вектор
получается вектор 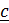 , модуль которого равен произведению модулей сомножителей на синус угла между ними:
, модуль которого равен произведению модулей сомножителей на синус угла между ними:
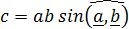 , а направлен он перпендикулярно сомножителям в ту сторону, откуда кратчайший поворот первого сомножителя ко второму виден: a) против часовой стрелки в правоориентированном пространстве;
, а направлен он перпендикулярно сомножителям в ту сторону, откуда кратчайший поворот первого сомножителя ко второму виден: a) против часовой стрелки в правоориентированном пространстве;
б) по часовой стрелке в левоориентированном.
Далее по умолчанию будем считать пространство правоориентированным. Отметим геометрический смысл векторного произведения – это вектор, перпендикулярный к сомножителям, длина которого равна площади построенного на них параллелограмма (рис. 1.4,a).
Из определения векторного произведения следует, что в результате умножения двух полярных или двух аксиальных векторов получается аксиальный вектор, а произведение полярного на аксиальный – полярный вектор.
Векторное произведение не зависит от системы координат, а его координатная форма записи зависит. Так, в ортонормированном базисе 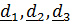 векторное произведение формально можно записать в виде определителя
векторное произведение формально можно записать в виде определителя
(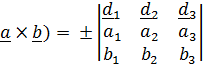 , (1.3)
, (1.3)
где знак (+) для правой тройки базисных векторов, а знак (–) – для левой.
Тройка векторов 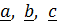 называется правой (в правоориентированном пространстве), если с конца третьего вектора (
называется правой (в правоориентированном пространстве), если с конца третьего вектора (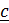 ) кратчайший поворот от первого (
) кратчайший поворот от первого (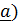 ко второму (
ко второму (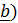 виден происходящим против часовой стрелки.
виден происходящим против часовой стрелки.
| Рис. 1.4. Векторное и смешанное произведения |
| b) |
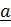 |
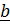 |
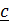 |
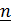 |
| S |
| a) |
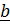 |
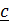 |
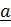 |
| S |
В заключение раздела приведем часто используемые в механике формулы смешанного и двойного векторного произведений.
Смешанное произведение (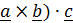 имеет простой геометрический смысл. Поскольку
имеет простой геометрический смысл. Поскольку 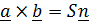 , где
, где 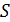 – площадь параллелограмма, а
– площадь параллелограмма, а 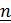 – единичный вектор нормали (рис. 1.4,b), то (
– единичный вектор нормали (рис. 1.4,b), то (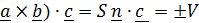 , где
, где 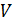 –объем параллелепипеда, построенного на векторах
–объем параллелепипеда, построенного на векторах 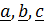 ; знак (+) соответствует случаю, когда тройка векторов
; знак (+) соответствует случаю, когда тройка векторов 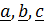 правая, знак (–) – левая.
правая, знак (–) – левая.
Смешанное произведение не изменяется при круговой перестановке:
(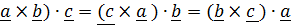 . (1.4)
. (1.4)
В координатном виде смешанное произведение с учетом (1.3) можно записать в виде:
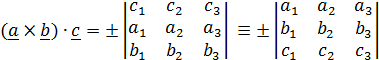 , (1.5)
, (1.5)
где, как и в (1.3), знак (+) для правой тройки базисных векторов, а (–) – для левой.
Формула для двойного векторного произведения имеет вид (без доказательства):
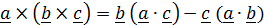 (формула «бац – цаб»). (1.6)
(формула «бац – цаб»). (1.6)
Упражнение 1.1. С помощью скалярного умножения доказать теорему косинусов для суммы векторов 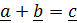 :
: 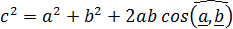
Упражнение 1.2. Доказать тождество (тождество Лагранжа):
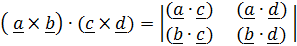 . (1.6a)
. (1.6a)
Обозначим 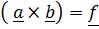 , внесем его по (1.4) в векторное произведение и воспользуемся тождеством (1.6):
, внесем его по (1.4) в векторное произведение и воспользуемся тождеством (1.6):
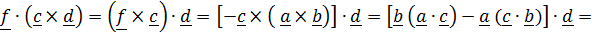
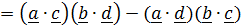 .
.
Полагая, в частности, 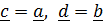 , получим:
, получим:
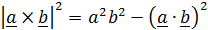 .
.
Упражнение 1.3. Доказать тождество
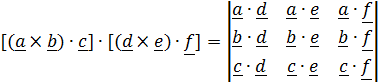 . (1.6б)
. (1.6б)
Разумеется, тождество (1.6b) можно проверить прямым вычислением с помощью (1.5), но можно поступить иначе, познакомившись заодно с понятием взаимного базиса. Обозначим для удобства 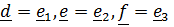 и разложим произвольный вектор по этому базису:
и разложим произвольный вектор по этому базису: 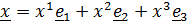 . Чтобы найти, например, координату
. Чтобы найти, например, координату 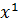 , надо умножить
, надо умножить 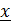 векторно на
векторно на 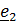 (исчезнет второе слагаемое) и затем скалярно на
(исчезнет второе слагаемое) и затем скалярно на 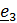 (исчезнет третье). Получим:
(исчезнет третье). Получим:
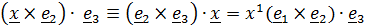 , откуда
, откуда 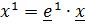 и аналогично
и аналогично 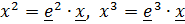 , где векторы
, где векторы
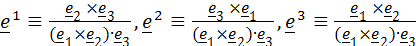 (1.6в)
(1.6в)
называются векторами взаимного базиса (или кобазиса). Таким образом,
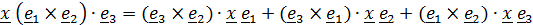 .
.
Примем теперь 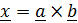 , заменим в правой части с помощью тождества Лагранжа произведения на
, заменим в правой части с помощью тождества Лагранжа произведения на 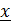 и умножим последнее равенство скалярно на
и умножим последнее равенство скалярно на 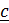 . Полученное выражение – разложение определителя (1.6б) по третьей строке.
. Полученное выражение – разложение определителя (1.6б) по третьей строке.
Если основной базис ортонормированный, то взаимный базис совпадает с основным, и только в этом случае координаты вектора совпадают с его проекциями на оси, задаваемые векторами базиса.
Формулы (1.6в) являются решениями системы уравнений 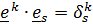 , из которой определяются векторы взаимного базиса. Независящий от выбора базиса вектор можно разложить как по основному базису:
, из которой определяются векторы взаимного базиса. Независящий от выбора базиса вектор можно разложить как по основному базису: 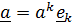 , так и по взаимному:
, так и по взаимному: 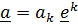 . Координаты
. Координаты 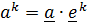 называются контрвариантными, а
называются контрвариантными, а 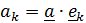 - ковариантными (при замене базиса они меняются по тому же закону, что и основной базис).
- ковариантными (при замене базиса они меняются по тому же закону, что и основной базис).
 2015-02-04
2015-02-04 819
819








