Кинематический расчёт кривошипно-ползунного механизма. Определение ускорений точек звеньев для заданного положения механизма

Дано:

1).Угловая скорость кривошипа является постоянной и равна .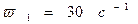

2).Размеры звеньев: ОА = 20мм, АВ = 76мм, ВС = 26мм, AS₂ = 51 мм.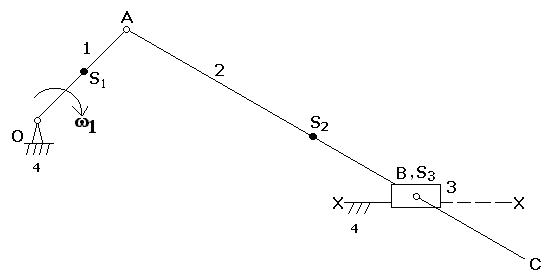

План ускорений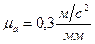

Исследуемая величина	Отрезок на плане	Направление	Величина отрезка на плане,	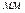Масштабный коэффициент	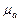Значение величины,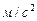

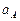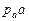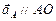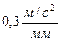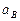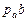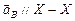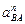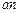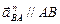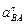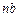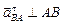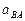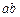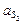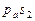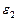1.Определение ускорения точки А.

Так как угловая скорость 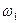является постоянной, то .

.

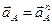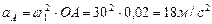Вектор ускорения 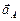направлен параллельно кривошипу ОА от точки А к точке О.

Выбираем масштаб плана ускорений 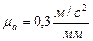. Найдём отрезок, изображающий вектор ускорения 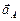на плане: 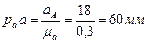. Из полюса плана ускорений 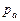откладываем данный отрезок в направлении, параллельном АО.

2.Определение ускорения точки В.

Запишем векторное уравнение: .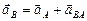

Вектор относительного ускорения 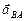раскладываем на нормальную и касательную составляющие: .

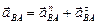Нормальное относительное ускорение равно:

.

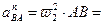
Найдём отрезок, изображающий вектор ускорения 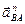на плане: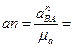

Продолжаем строить план ускорений. Вектор ускорения 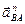направлен параллельно АВ. Откладываем отрезок 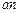из точки 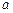плана ускорений в указанном направлении от точки В к точке А.

Вектор ускорения 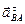направлен перпендикулярно АВ. Проводим это направление из точки 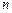плана ускорений.

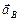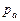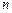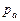Вектор ускорения направлен параллельно оси x – x. Проводим это направление из полюса . Две прямые линии, проведённые из точек и в указанных направлениях, пересекаются в точке .

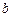Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб 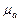, получим:

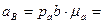
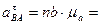
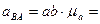
3.Определение ускорения точки .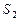

Воспользуемся следствием из теоремы подобия. Составим пропорцию:

,

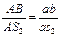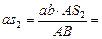
Данный отрезок откладываем на прямой 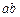от точки 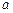. Точку 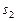соединяем с полюсом .

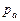Величина ускорения: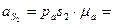

4.Определение углового ускорения шатуна АВ.

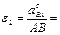
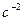. Для определения направления 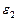переносим вектор 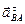в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует 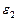. В данном случае угловое ускорение 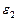направлено против часовой стрелки.