Устойчивость объектов и систем АСУ

В общем случае система или объект может быть описана с помощью дифференциального уравнения.

a_nyⁿ+…a₁y¹+a₀=b_mx^m+…b₁x`+b₀

Решение такого уравнения:

y(t)=y_общ(t)+y_ч(t)

y_общ(t)-для однородного;

y_ч(t)-для неоднородного.

Поскольку частное решение отражает вынужденное изменение координаты объекта под воздействием управления, то считается, что частное решение описывает невозмущенное движение. y(t) описывает возмущенное движение и тогда y_общ(t)

будет являться отклонением, т.е.

y_общ(t)=y(t)-y_ч(t)=x(t)

Возмущением будет являться y_общ(0). Для того чтобы объект был асимптотически устойчивым необходимо, чтобы

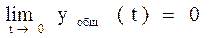
Общее решение будет стремиться к нулю в случае, если все действительные корни будут отрицательными, а действительные части комплексных корней меньше нуля. Если имеется хотя бы один корень с положительной действительной частью (находящееся в правой положительной полуоси) или правый корень, то решение и объект будут неустойчивыми.

Если имеются чисто мнимые корни, объект находится на границе устойчивости (возникают незатухающие колебания). Если имеются нулевые корни, в количестве больше 1 – объект неустойчив. Один нулевой – на границе устойчивости (апериодической)

1. 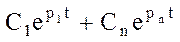- действительные и разные.

Если p- отрицательные →0

Если хотя бы один положительный – уходит в ∞.

2. корни кратные:

(C₁+C₂t+…C_mt^m-1)e^pT

если m-одинаковых корней

если p<0 → 0 (при t→ ∞)

если p положительное → 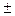∞ (в зависимости от знака коэффициента).

3. для пары комплексных корней

Ce^αtcos(βt+γ)

если α<0 затухающее колебание;

если α>0 расходящееся колебание.

4. Чисто мнимые.

Ccos(βt+γ)

амплитуда со временем не изменяется; C-определяется начальными условиями.

5. Нулевой корень.

1 нулевой корень С;

2 нулевых корня C₁t+C₂