Y = CX + DV
можно осуществить различными способами. Ниже приведем один из вариантов. Расчитаем таблицу W, содержащую N строк (обычно N=100 – 200) и n+1 столбцов, где n – число элементов вектора Y. Расположим в первом столбце (для примера) ток i6, во втором - uC, в третьем - uL, в четвертом – t.
Таблица W образуется с помощью подпрограммы
I6 = Z1<2>, uC = Z1<2>, uL = Z1<3>, t = Z1<4>
K = 1..N
Wk,1 = C11ik + C12uC,k + D1E
Wk,2 = C21ik + C22uC,k + D2E
Wk,3 = C31ik + C32uC,k + D3E
Wk,4 = tk.
3.3. Расчет переходных процессов в цепи с двумя
синусоидальными источниками энергии
Расчет переходного процесса осуществляется по той же методике, что и расчет переходного в процесса в цепи с постоянным источником. На рисунке 2.5 приведена схема с двумя источниками, полученная из схемы на рисунке 2.1 после коммутации.
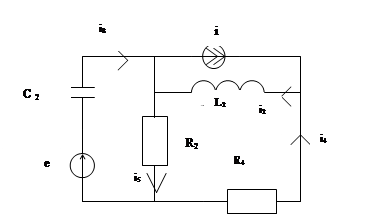
Рис. 2.5
Расмотрим подробнее расчет переходного процесса.
Составляется вектор независимых начальных условий i2(0) и u8(0), рассчитанные в разделе 2.2
X0 = [- 0.07 1.525]T.
На следущем этапе определяется длительность переходного процесса. Для этого составляется характеристическое уравнение. Предварительно находится операторное сопротивление в пассивной цепи относительно любых двух зажимов. Для схемы на рисунке 2.4 имеем
1 (L2p + R4)R2

 Z(p) = +.
Z(p) = +.
C2p R2 + R4 + L2p
 2015-03-07
2015-03-07 282
282








